wilcoxon

Синтаксис:

Y = wilcoxon(X, Y);

Аргументы:

Имя	Тип данных	Описание
X	`array`	Входной массив размерностью n
Y	`array`	Входной массив размерностью n

Описание:

wilcoxon – функция возвращает значение статистики, вычисленной по критерию Уилкоксона. Данный критерий используется для оценки различий между двумя выборками, взятыми из закона распределения, отличного от нормального, либо измеренными с использованием порядковой шкалы. Выдвигаются следующие предположения:

данные приходят парами – размерности выборок одинаковые;
пары независимы и одинаково распределены;
данные измерены хотя бы по порядковой шкале.

Нулевая гипотеза формулируется как: медиана разности между парами равна 0.

При этом n должно быть меньше 25, тогда критерий Уилкоксона можно уверенно использовать, при больших значениях распределение стремится к нормальному.

Значение статистики вычисляется по формуле:

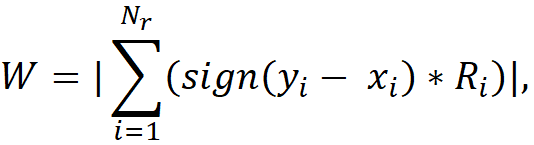
где R_i - ранг разности i-ой пары (y_i - x_i).

Если полученное значение W меньше критического, полученного по таблице, то основная гипотеза принимается, иначе отвергается.

Элементы векторов X, Y должны быть вещественными числами.

Входные массивы X, Y могут задаваться:

как переменные типа массив, определенные ранее:
Z = wilcoxon(X, Y);
как массивы, состоящие из переменных, определенных ранее:
Z = wilcoxon([x1,x2,x3,x4], [y1,y2,y3]);

Z = wilcoxon(X,[y1,y2,y3]);
Z = wilcoxon([x1,x2,x3,x4],Y);
как постоянные массивы:
Z = wilcoxon([0,0,2,1,0], [5,0,2,1,3]);

z = wilcoxon(X, [5,0,2,1,3]);

Z = wilcoxon([0,0,2,1,0], Y).

Результат:

Имя	Тип данных	Описание
Z	`double`	Значение статистики критерия

Пример:

const X = [125,115,130,140,140,115,140,125,140,135];
const Y = [110,122,125,120,140,124,123,137,135,145];
z = wilcoxon(X, Y);

В результате переменной z будет присвоено значение 9, представляющее собой значение статистики критерия. В данном случае при N_r = 9 (количество ненулевых пар) и уровне значимости α = 0.05 критическое значение равно 17. Так как полученное значение меньше критического, то основная гипотеза принимается, то есть разница между парами соответствует симметричному распределению вокруг нуля.

Дополнительные материалы

Нет.