mann_whitney

Функция вычисления значения статистики критерия Манна-Уитни.

Синтаксис

Z = mann_whitney(X, Y);

Аргументы

Имя Тип данных Описание
X array Входной массив размерностью n1
Y array Входной массив размерностью n2

Описание

mann_whitney – функция возвращает значение статистики, вычисленной по критерию Манна-Уитни.

Критерий Манна-Уитни используется для оценки различий между двумя независимыми выборками по уровню какого-либо признака, измеренного количественно. Позволяет выявлять различия в значении параметра между малыми выборками.

Ограничения применимости:
  1. В каждой из выборок должно быть не менее 3 значений признака. Допускается, чтобы в одной выборке было два значения, но во второй тогда не менее пяти.
  2. В выборочных данных не должно быть совпадающих значений (все числа — разные) или таких совпадений должно быть очень мало (до 10).

Статистика критерия:

где:

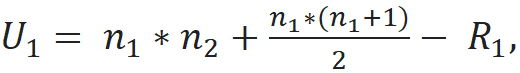
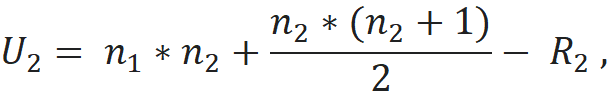
  • Ri - сумма рангов i-ой выборки.

По таблице для выбранного уровня статистической значимости определяется критическое значение для данных n1 и n2. Если полученное значение U меньше или равно табличному, то признается наличие существенного различия между уровнем признака в рассматриваемых выборках (принимается альтернативная гипотеза).

Если же полученное значение U больше табличного, то принимается нулевая гипотеза.

Достоверность различий тем выше, чем меньше значение U.

Элементы векторов X, Y должны быть вещественными числами.

Входные массивы X, Y могут задаваться:

  • как переменные типа массив, определенная ранее:

    Z = mann_whitney(X, Y);

  • как массив, состоящий из переменных, определенных ранее:

    Z = mann_whitney([x1,x2,x3,x4], [y1,y2,y3]);

    Z = mann_whitney([x1,x2,x3,x4], Y) ;

  • как постоянный массив:

    Z = mann_whitney([-1.80, -1.60, -1.40],Y);

    Z = mann_whitney(X,[-1.80, -1.60, -1.40]);

    Z = mann_whitney([-1.80, -1.60, -1.40],[-1.40, -0.78,-0.53,-0.35]);

Результат

Имя Тип данных Описание
Z double

Значение статистики критерия

Пример

const X = [88.94,96.74,99.3,110.57,113.98,123.58,216.28];
const Y = [98.19,102.84,103.7,103.93,106.96,110.05,110.39,126.72,134.82,153.6];
z = mann_whitney(X, Y);

В результате переменной z будет присвоено значение 32, представляющее собой значение статистики критерия. В данном случае при n1 = 7, n2 = 10 и уровне значимости α = 0.01 критическое значение равно 9. Так как полученное значение больше критического, то основная гипотеза отклоняется.

Дополнительные материалы

Нет.