ifft

Синтаксис:

Y = ifft(X);

Аргументы:

Описание:

ifft – функция вычисления обратного дискретного преобразования Фурье вектора X, вычисленного по алгоритму быстрого преобразования Фурье:

где: ω_N = e^(-2πi)/N , N - размерность вектора. Размерность вектора X должна быть степенью числа 2. Входной вектор может быть как массивом вещественных, так и массивом комплексных чисел. Комплексное число задается выражением a+bi, где a и b вещественные и мнимые части числа соответственно. Входной массив X может задаваться:

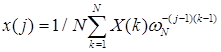
• как переменные типа массив, определенные ранее:

  Y = ifft(X);

• как массивы, состоящие из переменных, определенных ранее:

  Y = ifft([x1,x2,x3,x4]);

• как постоянные массивы:

  Y = ifft([1, 6, 4, 2]);

Результат:

Пример:

var Fs = 1000,// Частота   
Tt = 1/Fs,//Время
L = 1024;//Размер буфера
var t:array = 1024#0; //Вектор значения времени
var f:array = 1024#0; //Вектор значения частоты
var xn:array =1024#0;
for(i=0, L-1) t[i+1] = i*Tt; //заполним вектор времени
for(i=0, L-1) f[i+1] = i; //заполним вектор частоты
//Сумма синусоид 50 Гц и 120 Гц
x = 0.7*sin(2*pi*50*t) + sin(2*pi*120*t); 
//Добавим к сигналу случайный шум
for (i=0, L-1) xn[i+1]=x[i+1]+2*randg(0,1);
//дискретное преобразование Фурье
y = fft(xn);
y1 = abs(y);
//отфильтруем сигнал
// py – спектральная плотность сигнала
// Porog – порог для спектральной плотности
py = abs(y).*abs(y);
Porog = 4e4;
pz = 1024#(0,0);
//удалим сигнал выше порога
for (i=1,L)
if py[i] < Porog then pz[i]=0+0i 
else pz[i] = y[i];
//обратное преобразование Фурье (восстановление сигнала)
z=real(ifft(pz));

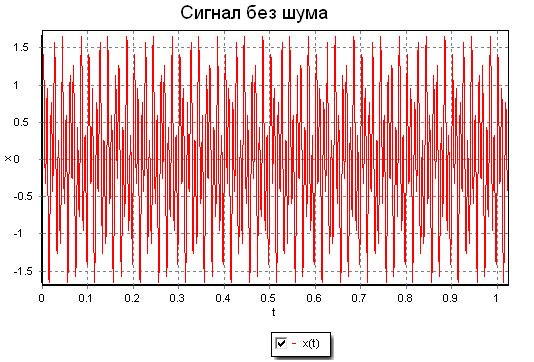
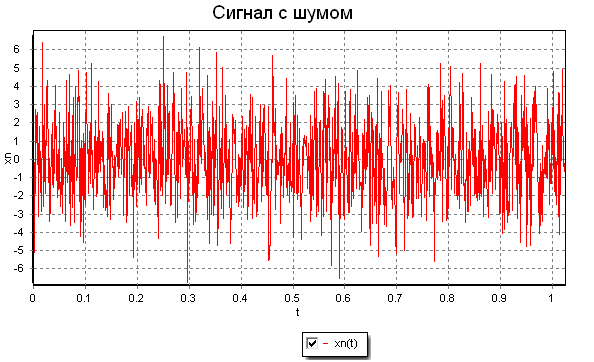
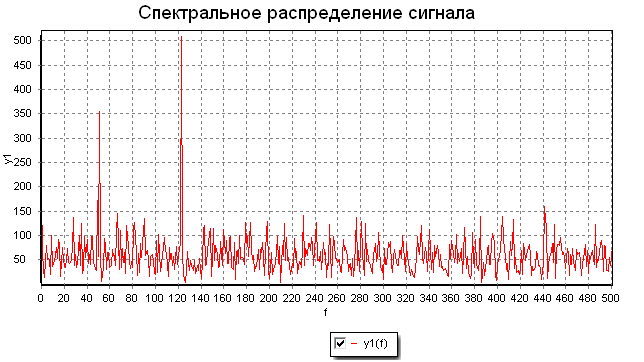
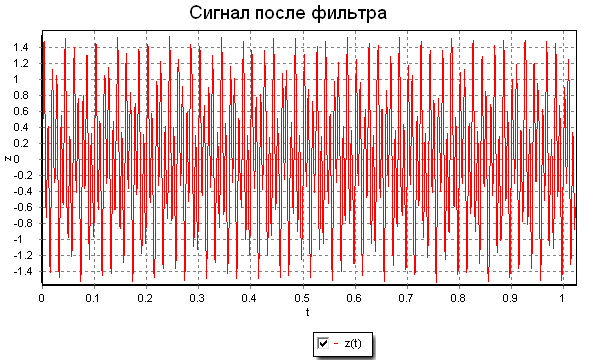
В примере формируется сигнал как сумма синусоид 50 Гц и 120 Гц (График «Сигнал без шума»). К нему добавляется случайный шум. По виду сигнала сложно определить частотные составляющие сигнала (График «Сигнал с шумом»). При помощи быстрого преобразования Фурье выделяются частотные составляющие спектра сигнала (50 Гц и 120 Гц, график «Спектральное распределение сигнала»). После происходит фильтрация спектра сигнала – отбрасывание сигнала ниже порога. При помощи обратного быстрого преобразования Фурье формируется исходный сигнал.

Дополнительные материалы

Нет.