fisher

Функция вычисления значения статистики критерия по критерию Фишера.

Синтаксис

Z = fisher(X, Y);

Аргументы

Имя Тип данных Описание
X array Входной массив размерности m
Y array Входной массив размерности n

Описание

fisher – функция возвращает значение статистики, вычисленной по критерию Фишера. Проверяется равенство дисперсий двух выборок объемом m и n случайных величин X и Y, имеющих нормальное распределение. Статистика критерия: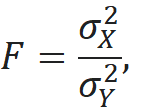

где: σ - среднеквадратичное отклонение.

При нулевой гипотезе статистика имеет распределение Фишера с (m-1) и (n-1) степенями свободы. Если статистика больше критического значения, соответствующего выбранному уровню значимости, то дисперсии случайных величин признаются не одинаковыми.

Элементы вектора X, Y должны быть вещественными числами.

Входные массивы X, Y могут задаваться:

  • как переменная типа массив, определенные ранее:

    Z = fisher(X, Y);

  • как массив, состоящий из переменных, определенных ранее:

    Z = fisher([x1, x2, x3, x4], [y1, y2, y3]);

    Z = fisher([x1, x2, x3, x4], Y);

    Z = fisher(X, [y1, y2, y3]);

  • как постоянный массив:

    Z = fisher([-1.80, -1.60, -1.40, -1.20], Y);

    Z = fisher(X,[-1.80, -1.60, -1.40, -1.20]);

    Z = fisher([-1.80, -1.60, -1.40, -1.20],[-1.40, -0.78,-0.53,-0.35]) ;

Результат

Имя Тип данных Описание
Z double

Значение статистики критерия

Пример

const X = [34,44,97,62,39,73,42,95,35,37,45,43,73,53,32];
const Y = [45,68,76,56,78,64,84,54,81,79,41,47,79,32,44];
z = fisher(X, Y);

В результате переменной z будет присвоено значение 1.5546053, представляющее собой значение статистики критерия. При m – 1 = 14, n – 1 = 14 и уровне значимости α = 0.05 критическое значение Fкрит = 2.49. Так как полученное значение меньше критического, то основная гипотеза принимается.

Дополнительные материалы

Нет.