Функция вычисления значения статистики критерия согласия Хи-квадрат (Пирсона).
Синтаксис:
Y = chi2_pearson(X);
Аргументы:
| Имя | Тип данных | Описание |
|---|---|---|
| X | array | Входной массив, содержащий элементы вектора |
Описание:
chi2_pearson – функция возвращает значение статистики, вычисленной по критерию Пирсона. Критерий согласия позволяет оценить значимость различий между фактическим (выявленным в результате исследования) количеством исходов или качественных характеристик выборки, попадающих в каждую категорию, и теоретическим количеством, которое можно ожидать в изучаемых группах при справедливости нулевой гипотезы. Статистика критерия согласия Пирсона определяется соотношением: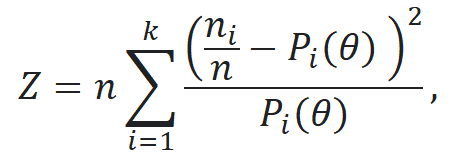
- ni - число элементов выборки, принадлежащих интервалу i;
- Pi(θ) - вероятность попадания в i-ый интервал, соответствующая теоретическому закону с функцией нормального распределения;
- k - число интервалов группировки.
При условии истинности H0 статистика имеет распределение Хи-квадрат со степенью свободы (k - 3). Если Z > Zкрит, то основная гипотеза отклоняется.
Элементы вектора X должны быть вещественными числами.
Входной массив X может задаваться:
- как переменная типа массив, определеннаяранее:
Y = chi2_pearson(X);
- как массив, состоящий из переменных, определенных ранее:
Y = chi2_pearson([x1, x2, x3, x4]);
- как постоянный массив:
Y = chi2_pearson([1.40, 0.78, -0.53, 0.35]);
Результат:
| Имя | Тип данных | Описание |
|---|---|---|
| Y | array |
Массив вида [значение статистики, вероятность, число интервалов группировки] |
Пример:
const X = [2#9 & 6#12 & 10#15 & 17#18 & 33#21 & 11#24 & 9#27 & 7#30 & 5#33]; y = chi2_pearson(X);
В результате переменной y будет присвоено значение [24.264989 , 0.99992932, 7] представляющее собой значение статистики и вероятность. Гипотеза о том, что данная выборка получена из нормально распределенной генеральной совокупности, не принимается, так как полученное значение статистики больше критического для k = 7 и α = 0.05.
Дополнительные материалы
Нет.
