cochren

Функция вычисления значения статистики по критерию Кохрена.

Синтаксис

Y = cochren(X);

Аргументы

Имя Тип данных Описание
X array2 Входная матрица размерности [m*L]

Описание

cochren – функция возвращает значение статистики, вычисленной по критерию Кохрена. Критерий Кохрена используется при сравнении трех и более выборок одинакового объема для проверки гипотезы о принадлежности нескольких дисперсий к одной генеральной совокупности, то есть формулируется основная гипотеза о равенстве дисперсий. Данные независимы и распределены по нормальному закону. Значение статистики для m образцов и L измерений:

где: - выборочная дисперсия m-ого образца в l-ой серии измерений.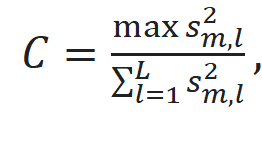

Если C < Cтабл, основная гипотеза принимается, дисперсия считается однородной, в противном случае — неоднородной.

Элементы матрицы X должны быть вещественными числами. Входная матрица X может задаваться:
  • как переменная типа матрица, определенная ранее:

    Y = cochren(X);

  • как матрица, состоящий из переменных, определенных ранее:

    Y = cochren([x1,x2],[x3,x4],[x5,x6]);

  • как постоянная матрица:

    Y = cochren([[0.1,2.0,2.3,1.2,0.8],[0,1.1,3.2,4.5,9.1]]);

Результат

Имя Тип данных Описание
Y array

Значение статистики критерия

Пример

Пусть имеется 4 объекта для каждого из которых произведено 8 измерений, как показано в таблице.

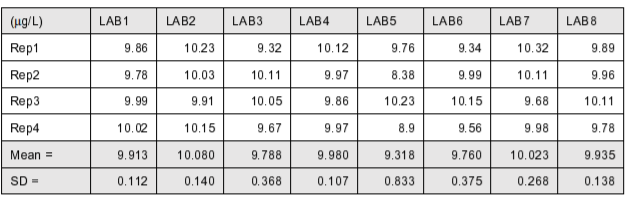
const X = [[9.86 ,10.23, 9.32, 10.12, 9.76, 9.34, 10.32, 9.89],
           [9.78 ,10.03, 10.11, 9.97, 8.38, 9.99, 10.11, 9.96],
           [9.99, 9.91, 10.05, 9.86, 10.23, 10.15, 9.68,10.11],
           [10.02, 10.15, 9.67, 9.97, 8.9, 9.56, 9.98,   9.78]];
y = cochren(X);

В результате переменной y будет присвоено значение 0.62856302, представляющее собой значение статистики критерия. При L = 8, m = 4 и уровне значимости α = 0.05 критическое значение Скрит = 0.438. Так как полученное значение больше критического, то основная гипотеза отклоняется, то есть среди выборок есть выборка с сильно преобладающей над другими дисперсией.

Дополнительные материалы

Нет.