fridman

Синтаксис:

Y = fridman(X);

Аргументы:

Имя	Тип данных	Описание
X	`matrix`	Входная матрица размерностью [n*k]

Описание:

fridman – функция возвращает значение статистики, вычисленной по критерию Фридмана. Для выборки из k измерений для каждого из n объектов проверяется гипотеза между полученными в разных условиях измерениями имеются лишь случайные различия, сравниваются средние для каждой из k групп, то есть нулевая гипотеза имеет вид: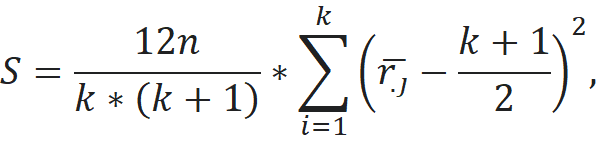

Статистика критерия:

где:

Если n ≥ 15 и k ≥ 4, то статистика имеет распределение Хи-квадрат с (k - 1) степенью свободы.

Количество измерений k должно быть одинаковым для каждого из объектов.

Элементы матрицы X должны быть вещественными числами.

Входная матрица X может задаваться:

как переменная типа матрица, определенная ранее:
Y = fridman(X);
как матрица, состоящая из переменных, определенных ранее:
Y = fridman([x1, x2], [x3, x4]);
как постоянная матрица:
Y = fridman([[0.1, 2.0, 2.3],[0,1.1,3.2],[1.1, 2.4, 5.9]]);

Результат:

Имя	Тип данных	Описание
Y	`double`	Значение статистики критерия

Пример:

const X = [[8,3,5,12],           
           [4,15,12,13],
           [6,23,15,20],
           [3,6,6,12],
           [7,12,3,8],
           [15,24,12,7]];
y = fridman(X);

В результате переменной y будет присвоено значение 5.75, представляющее собой значение статистики критерия. В данном случае n = 6, k = 4. При k – 1 = 3 и уровне значимости α = 0.05 критическое значение равно 7.815 Так как полученное значение меньше критического, то основная гипотеза об отсутствии значимых различий принимается.

Дополнительные материалы

Нет.