besselk

Синтаксис

y = besselk(v, x);

Аргументы

Описание

Линейное обыкновенное дифференциальное уравнение второго порядка вида:

называется уравнением Бесселя. Число v называется порядком уравнения Бесселя. Модифицированное уравнение Бесселя, которое получается из регулярного уравнения Бесселя заменой x на –ix, имеет вид:>

Решение данного уравнения выражается через так называемые модифицированные функции Бесселя первого и второго рода:

где C₁ и C₂ − произвольные постоянные, I_v(x) и K_v(x) обозначают модифицированные функции Бесселя, соответственно, первого и второго рода.

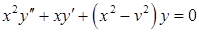
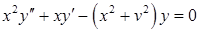
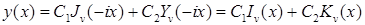
Функция besselk вычисляет модифицированную функцию Бесселя второго рода K_v(x) порядка v от аргумента x.

Результат

Пример

input x;  //вход - аргумент
output y; //выход - значение модифицированной функции Бесселя второго рода
v = 2;
y = besselk(v, x);

В результате выполнения скрипта переменной y будет присвоено значение модифицированной функции Бесселя второго рода второго порядка.

Дополнительные материалы

Нет.