Полное движение с учетом вращения Земли

в палитре на схеме

Описание

Допустим, что управление в каждый момент времени совмещает продольную ось ракеты с вектором скорости. При хорошо работающем управлении колебания ракеты относительно центра масс можно не учитывать и рассматривать движение ракеты как материальной точки.

Дифференциальное уравнение движения центра масс в инерциальной системе координат и обозначениях формулы имеет вид:

В относительном движении:

Проекция силы тяги на координатные оси будет равна произведению силы Тяги на косинус угла между направлением век­тора силы и соответствующей осью. Косинусы углов будут равны соответственно:

где: vreg. x, vreg.y и vreg. z - проекции скорости относительного движения центра массы ракеты на координатные оси. Опуская в дальнейшем индексы "отн", получим:

Проекции силы тяги определяются формулами:

Проекции аэродинамических сил на координатные оси будут равны силе R, умноженной на косинусы углов между направлением вектора силы тяги и соответствую­щей координатной осью:

Составляющие силы тяготения Земли определим, пользуясь формулой для ускорения силы земного тяготения, полученной в предположении, что Земля - шар:

где т0 - ускорение силы земного тяготения у поверхности Земли; RE - радиус Земли; r - расстояние от центра масс ракеты до условного центра Земли.

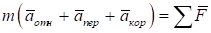
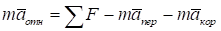
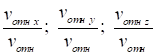
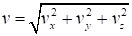
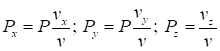
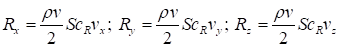
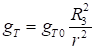
Составляющие силы земного тяготения будут равны:

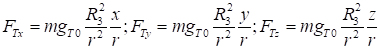
где x/r, y/r, z/r - косинусы углов между направлением действия силы FT и соответствующей координатной осью.

Используя данные формулы, получим систему дифференциальных уравнений, описывающих движение центра масс ЛА:

и

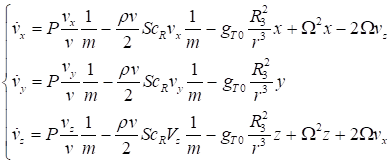
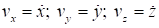
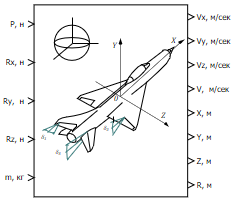
Входные порты

  • P - значение силы тяги [Н];
  • Rx, Ry, Rz - проекции аэродинамических сил на соответствующие оси геоцентрической СК [Н];
  • m - масса ЛА [кг].

Выходные порты

  • Vx, Vy, Vz - проекции относительной скорости на оси геоцентрической СК [м/сек];
  • V - модуль вектора относительной скорости [м/сек];
  • X, Y, Z - геоцентрические координаты ЛА [м];
  • R - радиус вектор ЛА относительно центра сферической Земли [м].

Свойства

  • Vx0, Vy0, Vz0, X0, Y0, Z0 - начальное состояние ЛА - начальные значения трех скоростей по соответствующим осям геоцентрической СК и трех координат.

Параметры

Блок не имеет параметров.

Сопутствующие материалы

  • Динамика полета беспилотных летательных аппаратов. А.А. Лебедев, Л.С. Чернобровкин Изд. "Машиностроение" 1973
  • Внешняя баллистика. А.А. Дмитриевский Изд. "Машиностроение" 1972