Боковое движение упрощенное

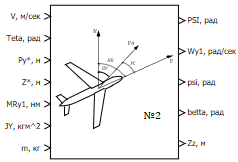
в палитре на схеме

Описание

При разделении сложного движения ракет на продольное и боковое принимают, что в первом приближении продольное движение не зависит от бокового. В соответствии с этим в уравнениях для определения характеристик продольного движения учитывают только те силы и моменты, которые действуют в плоскости стрельбы. При определении же характеристик бокового движения ракеты считать его независимым от продольного нельзя, поэтому в уравнения включаются все силы и моменты, которые в той или иной степени могут вызвать отклонения ракеты от плоскости стрельбы.

Система уравнений, описывающую боковое движение центра масс ракеты в полускоростной системе координат 0XY*Z*:

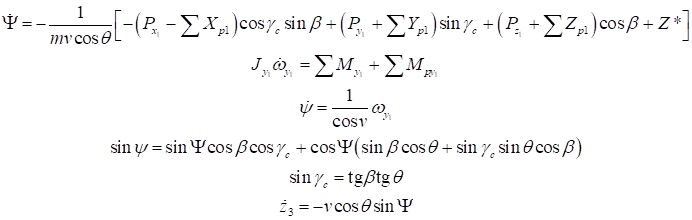
Уравнения, описывающие только боковое движение, не могут решаться самостоятельно, без учета основных величин, определяемых продольным движением. Например, в системе первое уравнение является основным при определении параметров бокового движения, но оно решается, только если известны m(t), v(t) и 0(t). Аэродинамические силы, и моменты, действующие в боковом направлении, также не могут быть определены, если не известны скорость и высота полета.

При больших углах наклона траектории необходимо проверять пределы применимости формулы, определяющей ɣc.

Существенное упрощение системы можно получить, если применить искусственный прием и принять углы тангажа и наклона траектории равны 0 в уравнениях, определяющих угловые параметры движения ракеты. Такое допущение равносильно, предположению, что ракета летит в горизонтальном положений, продольная ось ее составляет с вектором скорости центра масс угол р, а угол ɣc=0.

Для получения результатов, близких к действительным, в уравнениях, определяющих условную горизонтальную траекторию движения центра масс ракеты, скорость ее должна быть взята равной v*cos(θ), множители которой определяются при решении системы уравнений, описывающих продольное движение центра масс ракеты (снаряда). При принятых допущениях из системы дифференциальных уравнений, приведенных выше следует более простая система ДУ:

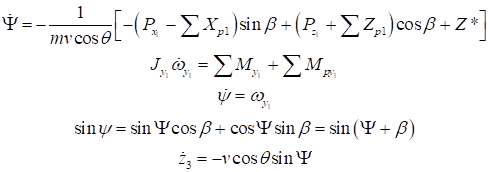
Предпоследнее равенство можно заменить суммой углов:

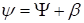
Входные порты

  • V - модуль скорости ЛА размерность [м/c];
  • Teta - угол наклона траектории размерность [рад];
  • Pz* - тяга двигателя ЛА в проекции на полускоростную ось 0Z*;
  • Z* - аэродинамическая сила на ось 0Z*;
  • MRy1 - проекция момента в связанной системе координат на ось Y1 размерность [Нм];
  • Jy1 - моменты инерции ЛА размерность [кг*м^2];
  • m - масса ЛА размерность [кг].

Выходные порты

  • PSI - угол поворота траектории размерность [рад];
  • Wy1 - угловая скорость вращения ЛА относительно связанных осей размерность [рад/сек];
  • psi - угол рысканья размерность [рад];
  • betta - угол скольжения размерность [рад];
  • Gamma_с - угол крена (угол между плоскостями 0X1Y1 и 0XY*) размерность [рад];
  • Zz - боковое смещение размерность [м].

Свойства

  • BigPsi0 - начальное значение угла поворота траектории [град];
  • Wу01 - начальные значения скоростей вращения ЛА [рад/сек];
  • Z0 - начальные значения бокового смещения размерность [м];
  • psi0 - начальное значение угла рысканья размерность [град].

Параметры

Блок не имеет параметров.

Сопутствующие материалы

  • Динамика полета беспилотных летательных аппаратов. А.А. Лебедев, Л.С. Чернобровкин Изд. "Машиностроение" 1973
  • Внешняя баллистика. А.А. Дмитриевский Изд. "Машиностроение" 1972