Описание демо-примера
Расположение
C:\SimInTech64\Demo\Автоматика и математика\Математические задачи\Аттракторы\Аттрактор Рёсслера
Описание
Аттрактор Рёсслера — хаотический аттрактор, которым обладает система дифференциальных уравнений Рёсслера:
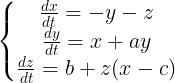
При значениях параметров a=b=0.2 и 2.6≤c≤4.2 уравнения Рёсслера обладают устойчивым предельным циклом. При этих значениях параметров период и форма предельного цикла совершают последовательность удвоения периода.
Сразу же за точкой c=4.2 возникает явление хаотического аттрактора. Чётко определённые линии предельных циклов расплываются и заполняют фазовое пространство бесконечным счетным множеством траекторий, обладающим свойствами фрактала. Сам Рёсслер изучал систему при постоянных a=0.2, b=0.2 и c=5.7, но также часто используются и значения a=0.1, b=0.1, и c=14.
- a≤0: Сходится к устойчивой точке.
- a=0.1: Крутится с периодом 2.
- a=0.2: Хаос .
- a=0.3: Хаотичный аттрактор.
- a=0.35: Аналогичен предыдущему, но хаос проявляется сильнее.
- a=0.38: Аналогичен предыдущему, но хаос проявляется ещё сильнее.
Зафиксируем a=b=0.1 и будем изменять c. При маленьких c система периодична, но при увеличении быстро становится хаотичной. Например, при c = 4 аттрактор будет иметь период равный единице, и на диаграмме будет одна единственная линия, то же самое повторится когда c = 3 и так далее, пока c не станет больше 12: последнее периодичное поведение характеризуется именно этим значением, дальше повсюду идёт хаос.
