Описание демо-примера
Расположение
C:\SimInTech64\Demo\Автоматика и математика\Гибридные системы\Кольцевой модулятор
Описание
Решение задачи Коши для системы дифференциальных уравнений кольцевого модулятора является отличным примером реальной задачи математического моделирования в технических системах высокой жёсткости. Электрическая схема кольцевого модулятора приведена на рисунке ниже (Рисунок 1). Получая на входе низкочастотный сигнал Uin1 и высокочастотный сигнал Uin2, кольцевой модулятор генерирует на выходе смешанный сигнал U2.
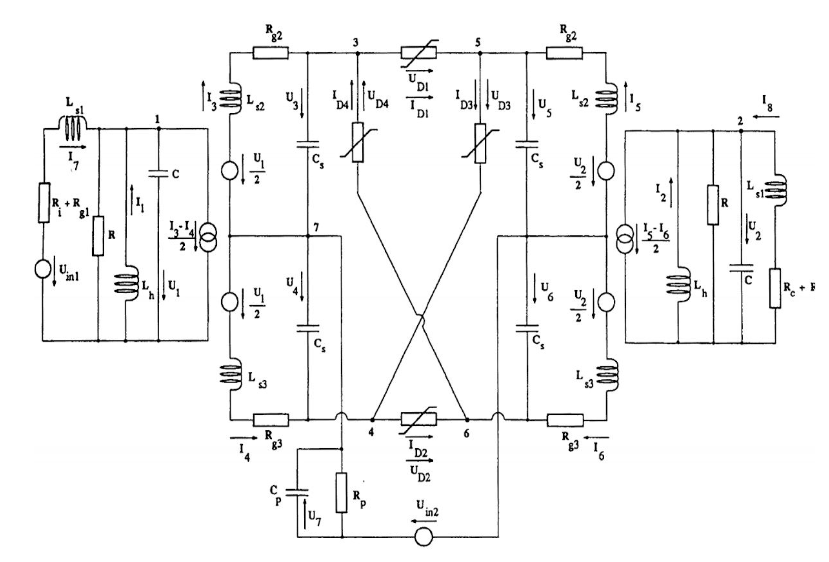
Рисунок 1. Электрическая схема кольцевого модулятора
Каждый конденсатор, входящий в радиоэлектронную схему, приводит к появлению дифференциального уравнения CU'=I. Применение первого правила Кирхгофа для электрической цепи приводит к дифференциальным уравнениям:
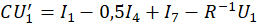
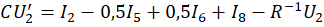
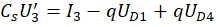
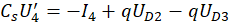
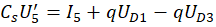
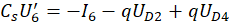
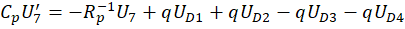
где
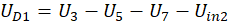
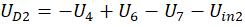
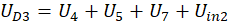
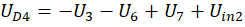
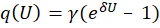, где
γ и δ – константы. Каждый индуктор также приводит к дифференциальному
уравнению LI'=U. Применение второго правила Кирхгофа к замкнутой цепи, содержащей
индуктор, приводит к восьми дифференциальным уравнениям:
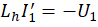
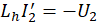
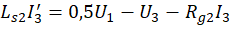
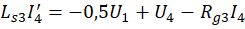
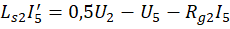
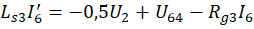
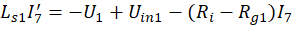
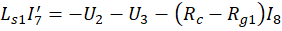
В начальный момент времени напряжения и силы токов отсутствуют, следовательно, начальные условия по всем переменным равны нулю. Отождествляя напряжения с yi, 1 ≤i ≤7, и силы токов с yi, 8 ≤i ≤15, то есть, полагая
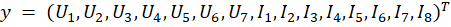
получим пятнадцать дифференциальных уравнений:
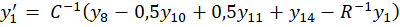
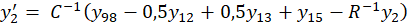
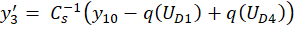
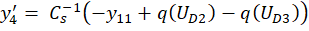
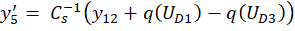
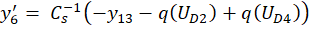
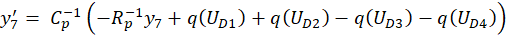
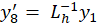
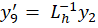
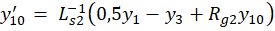
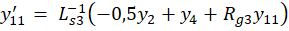
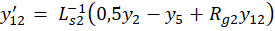
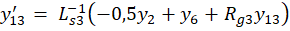
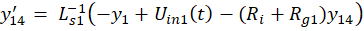
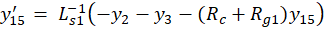
где y ∈R15; y(0)=0; 0≤t≤10-3.
Вспомогательные функции UD1, UD2, UD3, UD4, q, Uin1 и Uin2 задаютс формулами:
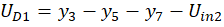
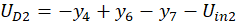
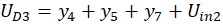
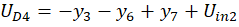
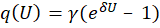
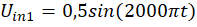
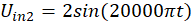
Расчеты проводились со следующими параметрами: C=1.6*10-8; CS=2*10-12; Cp=10-8; LS1=0.002; LS2=5*10-4; LS3=5*10-4; γ =40.67286402*10-9; δ=17.7493332; R=25000; Rp=50; Rg1=36.6; Rg2=17.3; Rg3=17.3; Ri=50; Rc=600.
Для тестирования была создана программная модель в среде моделирования SimInTech со следующими параметрами:
- Минимальный шаг – 10-14;
- Максимальный шаг – 10-6;
- Абсолютная ошибка – 2*10-6;
- Относительная ошибка – 2*10-6;
- Время моделирования (t) – 10-3.
Результаты моделирования приведены в таблице.
| Метод | Время расчёта (с) |
| RK23 | Нет данных |
| RK23ST | 4:39:00 |
| RKF78 | 2:31:17 |
| RKF78ST | Нет данных |
| Адаптивный 1 | 6:03 |
| Адаптивный 4 | 0:17 |
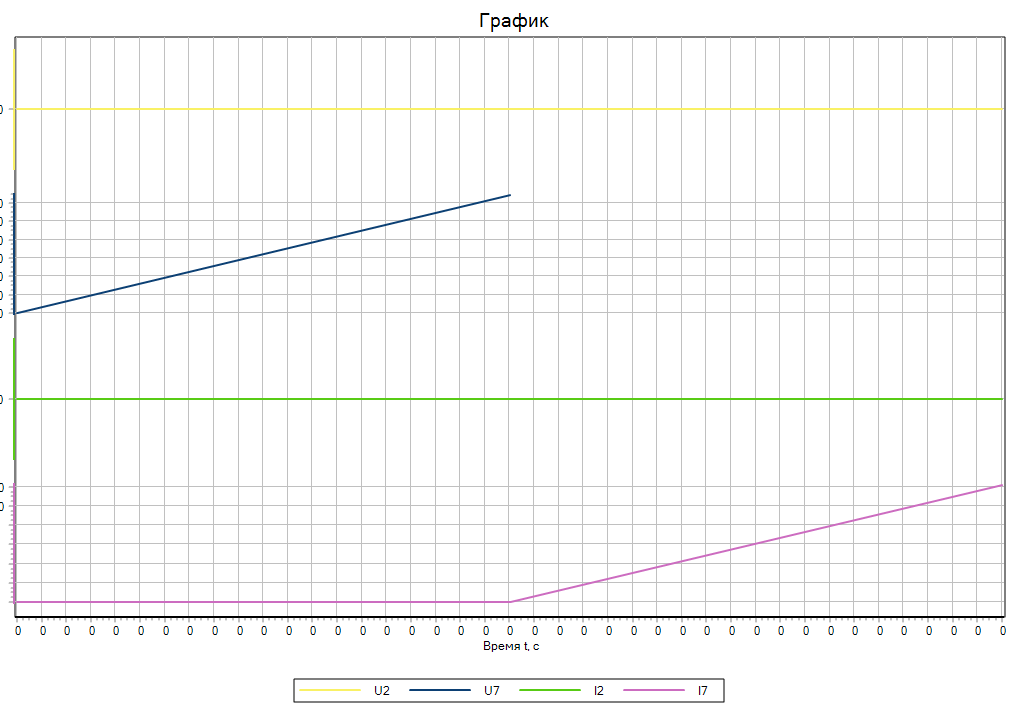
Рисунок 2. Результаты моделирования методом RK23
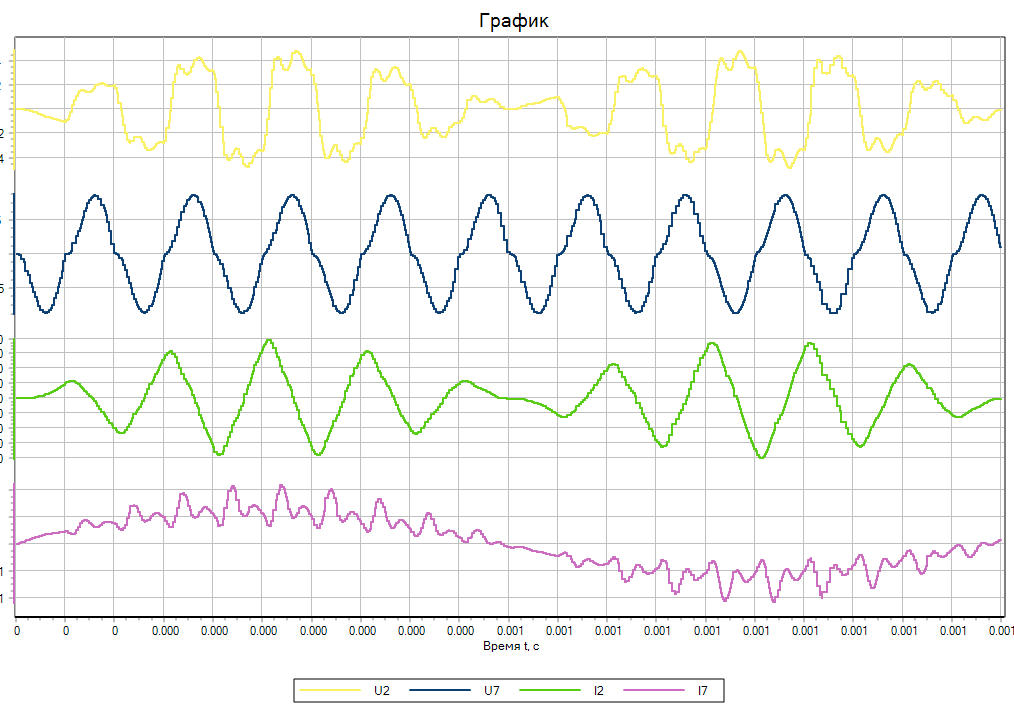
Рисунок 3. Результаты моделирования методом Адаптивный 1
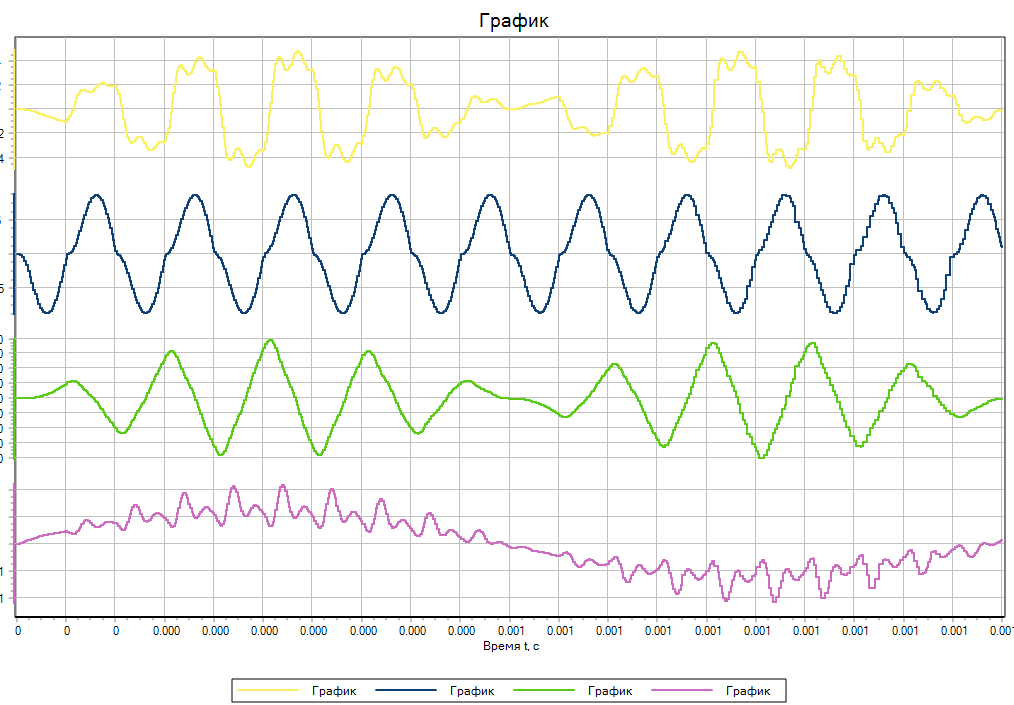
Рисунок 4. Результаты моделирования методом RK23ST
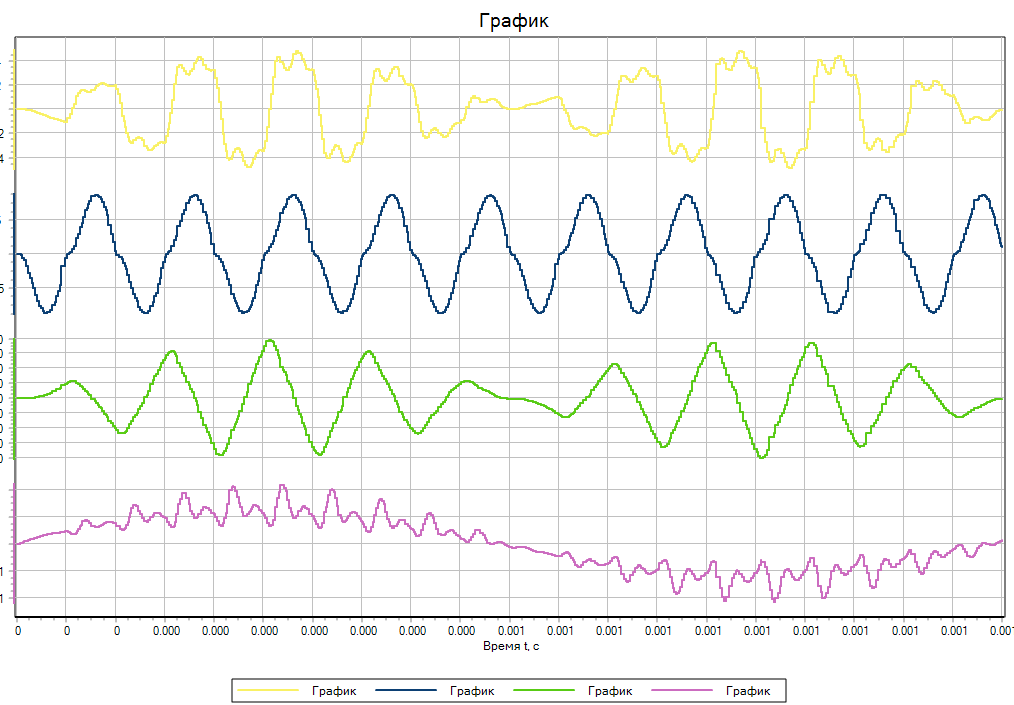
Рисунок 5. Результаты моделирования методом RKF78
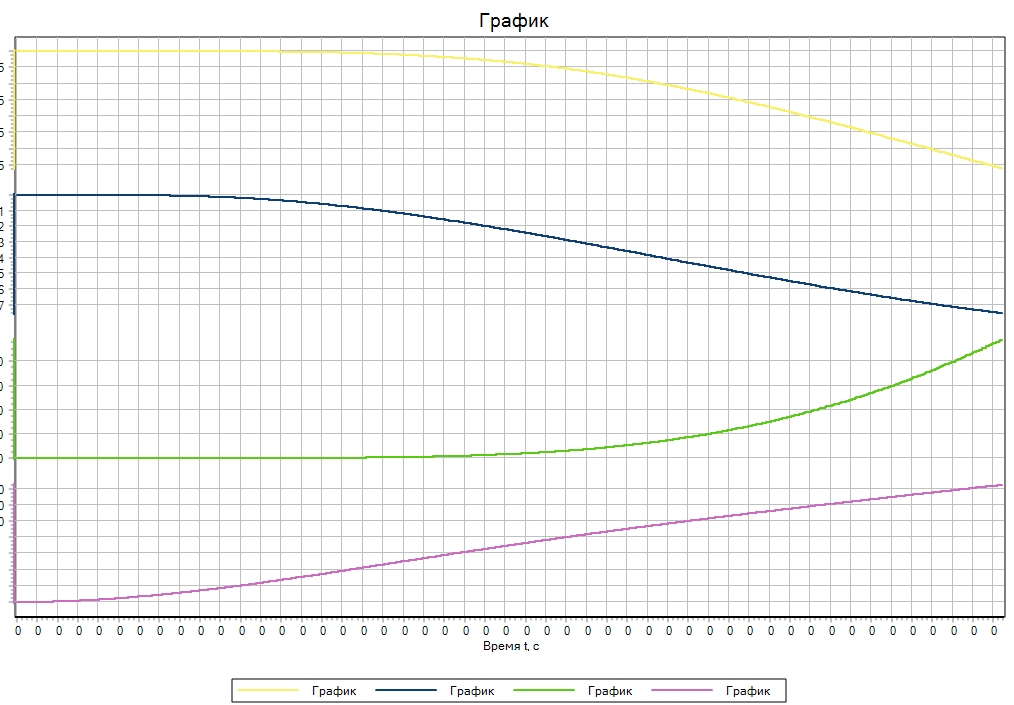
Рисунок 6. Результаты моделирования методом RKF78ST
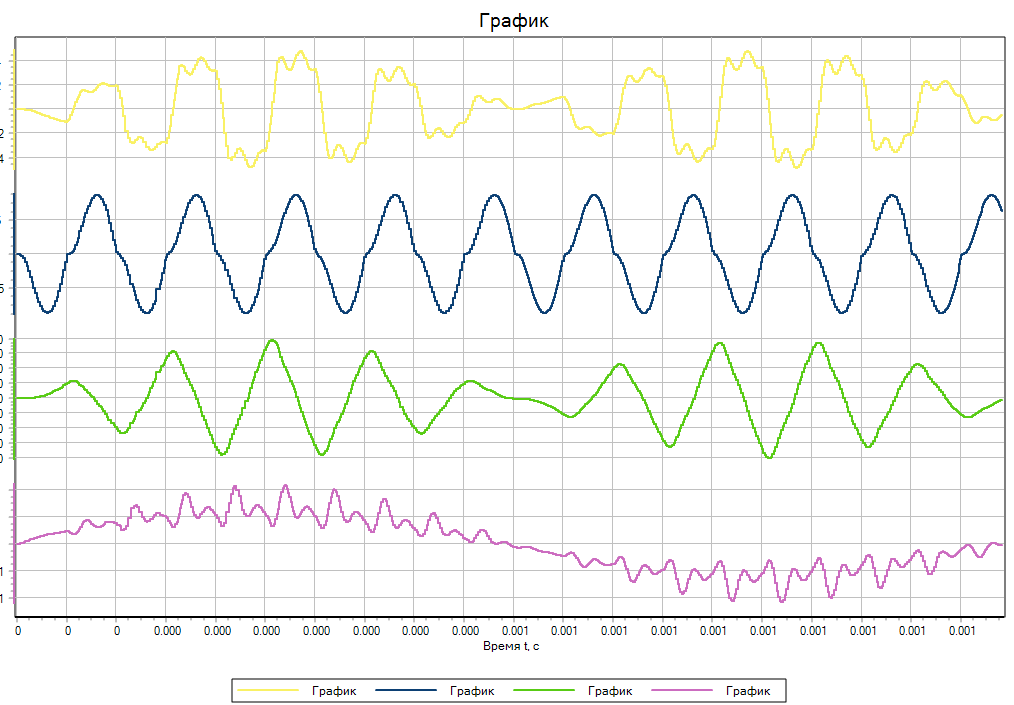
Рисунок 7. Результаты моделирования методом Адаптивный 4
Результаты моделирования продемонстрированы на рисунках (Рисунок 2, Рисунок 3,Рисунок 4, Рисунок 5, Рисунок 6, Рисунок 7). По результатам, метод RK23 не смог верно рассчитать данную задачу в виду отсутствия проверки на устойчивость, что позволило методу RK23ST провести моделирование корректно. Все методы, кроме RK23, показали схожие результаты. Однако, время расчёта методом Адаптивный 4 было значительно ниже, чем у RK23ST, RKF78. В таблице (Таблица 1)приведены времени расчёта для каждого метода. Адаптивные методы с существенно жесткими задачами высокой размерности в данном случае справились значительно лучше, чем RK23ST и RKF78.
