Адаптивный 4

Многошаговый адаптивный метод переменного порядка (от 1-го до 5-го для жестких задач и от 2-го до 6-го для нежестких задач),основанный на использовании разделенных разностей, определяемых рекуррентно согласно формулам

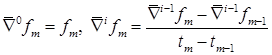
(аналогично определяются ∇ⁱx_m ).Введем также коэффициенты a_ij, g_i , зависящие от размеров текущего и предыдущих шагов и задаваемые формулами

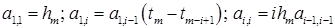
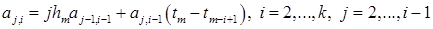
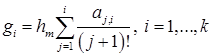
В этом случае k-шаговые формулы прогноза и коррекции при интегрировании с переменным шагом запишутся в виде

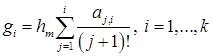
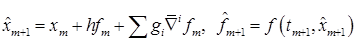
где ∇^kf_m+1 – разделенная разность с использованием ḟ_m+1 вместо f_m+1. Формула прогноза имеет порядок k, а порядок формулы коррекции на 1 больше.

На основе формул вида (*) обычно строят многошаговые методы переменного порядка и шага, при этом принимается x_m+1=ẋ_m+1, а оценка ошибки получается как разность между прогнозом и скорректированным решением. Для адаптивного метода эти формулы являются предварительными, на их основе можно получить вектор оценок наибольшего собственного значения:

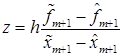
Чтобы предотвратить деление на ноль, вместо z вычисляем вектор

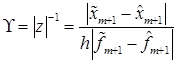
причем только для жестких и неустойчивых компонент, удовлетворяющих условию

где μ – константа, определяемая областью устойчивости и зависящая от k. Формула интегрирования для таких компонент имеет вид

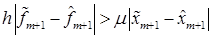
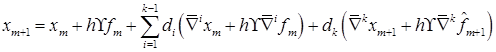
где векторные коэффициенты d_i вычисляются по формулам

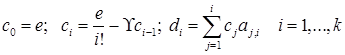
(e – n-мерный вектор с единичными компонентами).

Формула (*) построена таким образом, что она имеет порядок k и обеспечивает затухание за один шаг при решении уравнения x'= λx, λ<0.

Формулы (*)–(*) задают многошаговый адаптивный метод с переменным шагом, при этом для нежестких компонент ограничиваемся формулами (*), и дальнейшие вычисления не производим. Оценку ошибки получаем как приращение в формуле коррекции (*) для нежестких компонент или последний член в формуле (*) для жестких компонент. Приведенные формулы позволяют также легко изменять порядок метода, который определяется значением k, т.е. числом членов в формулах (*), (*). Если на предыдущем шаге было k=k_old , то на очередном шаге значение k может быть от 1 до k_old+1. Новое значение k определяется на этапе прогноза исходя из условия, чтобы прогноз был наиболее точным. Формулу прогноза (*) можно записать в виде

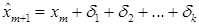
Новое значение k определяется как максимальное число, для которого выполняется условие

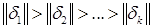
где норма ошибки вычисляется в соответствии с (*).