Анализ топологии структурной схемы

Анализируя информационные потоки в структурной схеме, можно определить сам факт взаимосвязи входа одного блока с выходом другого блока, но нельзя ничего сказать о характере этой связи. Характер связи определяется особенностями модели самого блока, а именно тем, как влияет тот или иной вход блока на его выход.

Если выход блока явно зависит от его входов, то на момент расчета этого блока все его входы должны быть определены. В математической модели таких блоков уравнения для выходов имеют следующий вид:

Примером блоков такого типа является усилитель сигнала, передаточная функция общего вида, где порядок числителя равен порядку знаменателя, блок Переменные состояния с ненулевой матрицей D и т.д.

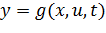
Если в математической модели блока уравнение для выхода имеет вид

то такой блок называется приоритетным. Выходы приоритетных блоков являются функцией только их внутренних атрибутов (параметров и состояний блока). Примерами приоритетных блоков являются источники сигнала, динамические блоки и т.д.

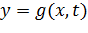
Объединяя уравнения вида (*) и (*) всех блоков структурной схемы и, учитывая, что входным сигналом блока является выход другого блока или переменная, зависящая от модельного времени t, получим уравнения всей системы в виде:

где х - вектор всех переменных состояния, y - вектор выходных переменных всех блоков модели.

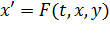
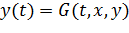
При реализации методов численного интегрирования необходимо получить уравнения моделируемой системы в нормальной форме Коши, то есть в виде

Опишем процедуру приведения уравнений к форме Коши. Отметим, что не обязательно получать явные выражения в виде (*-*), достаточно сформировать процедуру, которая позволяет по заданным значениям модельного времени t и вектора переменных состояния x вычислить вектор производных x’ и вектор выходов у. Идея этой процедуры – упорядочение (сортировка) всех блоков таким образом, чтобы выход очередного блока мог быть рассчитан по уже имеющейся к этому моменту информации. Практически сортировка позволяет получить уравнения выходов блоков в виде (*). Затем производные могут быть рассчитаны с использованием (*).

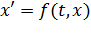
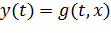
Перед началом сортировки будем считать, что нам известны t и x. В процессе сортировки будет сформирован упорядоченный список, содержащий в общем случае 5 групп блоков и соответствующих им выходных переменных.

1. Сначала выделим и упорядочим все блоки, выходы которых могут быть рассчитаны по известному модельному времени t:

   

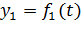
2. Далее выделим и упорядочим все блоки, выходы которых могут быть рассчитаны по известным t, x, y₁. Это соответствует записи

   

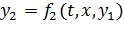
   Этот этап завершает первичную сортировку. Если система не имеет алгебраических контуров, то все блоки структурной схемы к этому моменту станут упорядоченными, и процедура будет завершена, если нет – следует продолжить упорядочение.

3. Выделим все блоки, непосредственно входящие в алгебраические контуры. Из них выделим определяющие (y₄). Выходы остальных входящих в алгебраические контуры блоков (y₃) можно рассчитать по известным выходам уже упорядоченных и определяющих блоков:

   

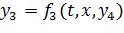
   Метод выделения определяющих переменных рассматривается ниже.

4. Поместим в список определяющие блоки, выходы которых запишутся в виде
   

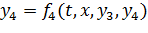
   Можно исключить y₃ из (*), однако приведенная запись позволяет лучше понять рассмотренные ниже схемы расчета алгебраических контуров.

5. В последнюю очередь рассчитываются блоки, не входящие в алгебраические контуры, но выходы которых зависят от блоков, входящих в алгебраические контуры:

   
   В результате сортировки будет получен такой порядок расчета блоков, который соответствует использованию формул (*)…(*). Если в модели нет алгебраических контуров, можно по известным t, x найти выходы всех блоков, в противном случае следует решать алгебраические уравнения относительно определяющих переменных y₄.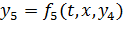

Расчет алгебраических контуров можно выполнить по следующим итерационным схемам.

Метод простых итераций:

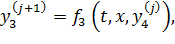
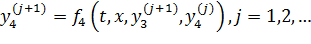
Метод Ньютона:

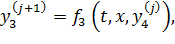
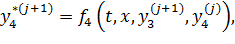
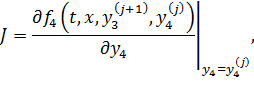
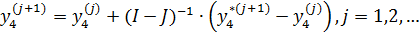
В общем случае матрица Якоби J может не обновляться в течение нескольких итераций (модифицированный метод Ньютона).

Алгоритм расчета выходов блоков и производных переменных состояния запишется следующим образом:

1. По известным t, x, используя (*), (*), рассчитать y₁, y₂.

2. Используя итерационную схему (*) или (*), найти y₃, y₄.

3. Используя (*), вычислить y₅.

4. Рассчитать производные переменных состояния всех динамических блоков.