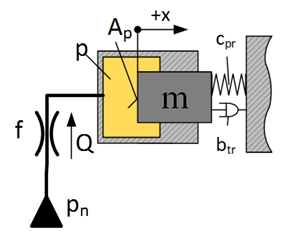
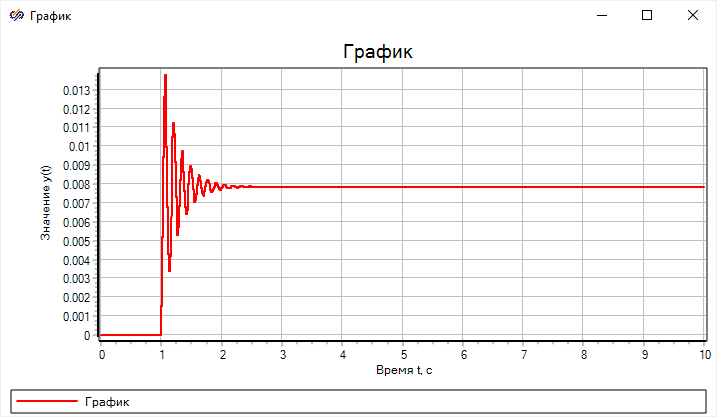
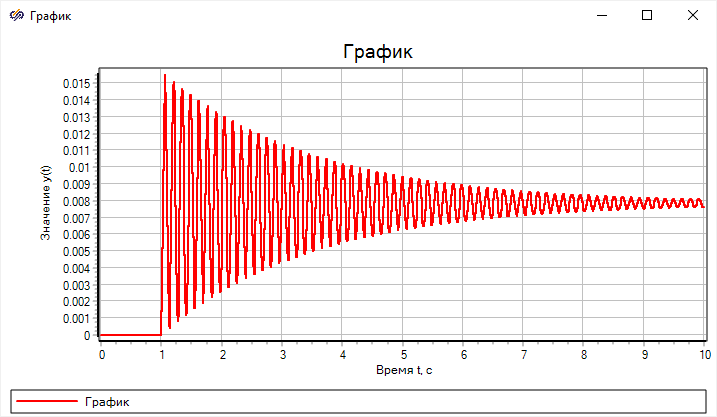
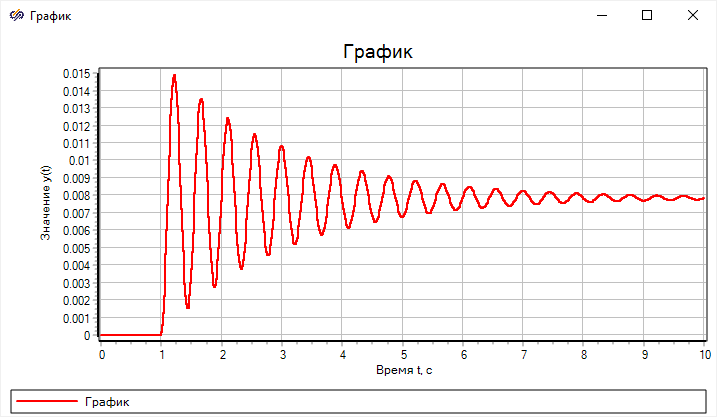
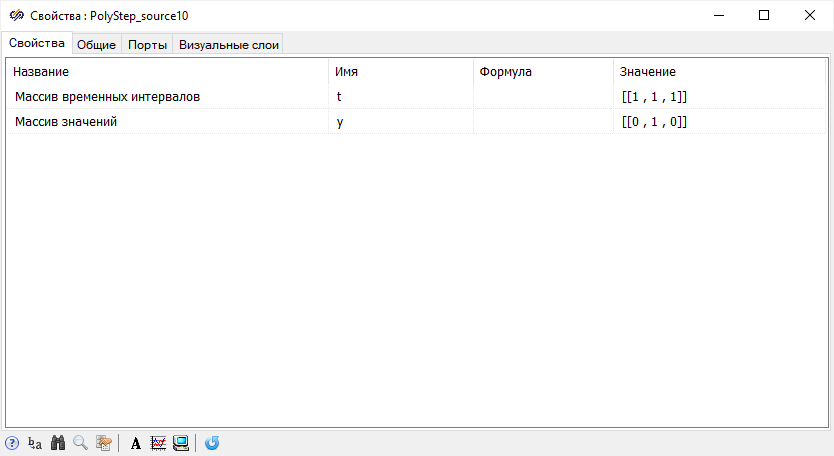
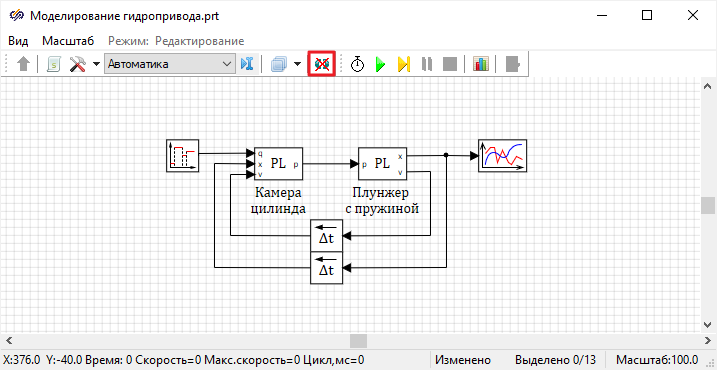
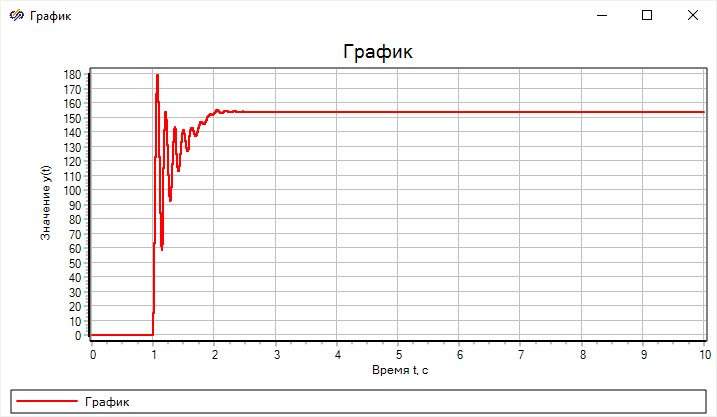
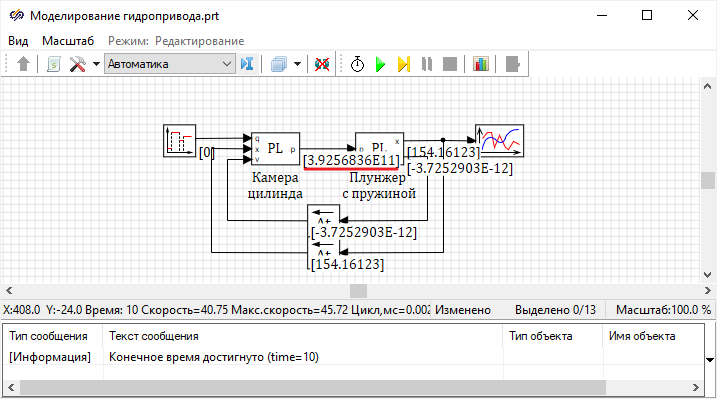
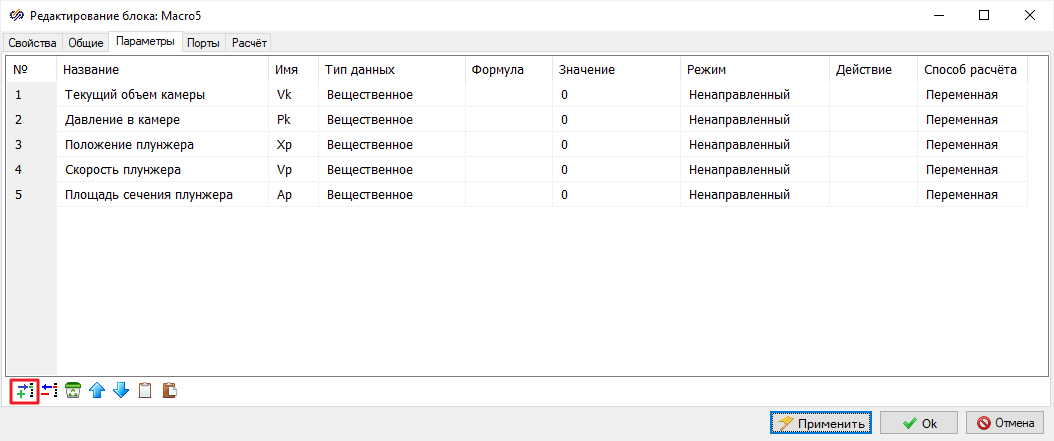
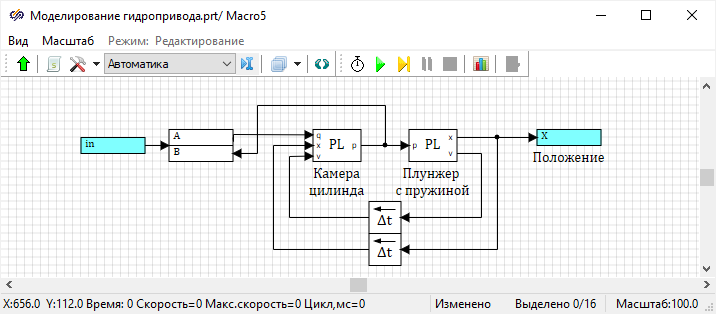
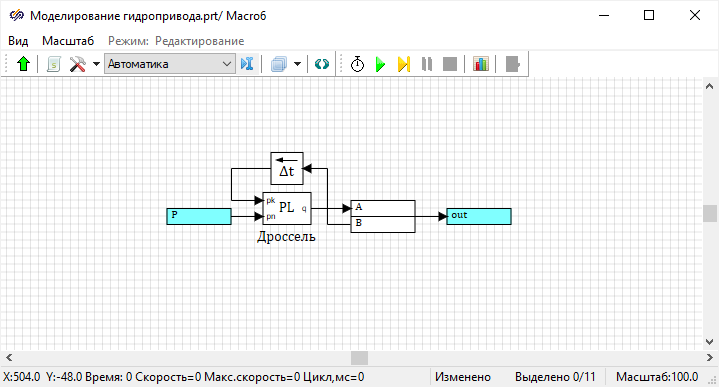
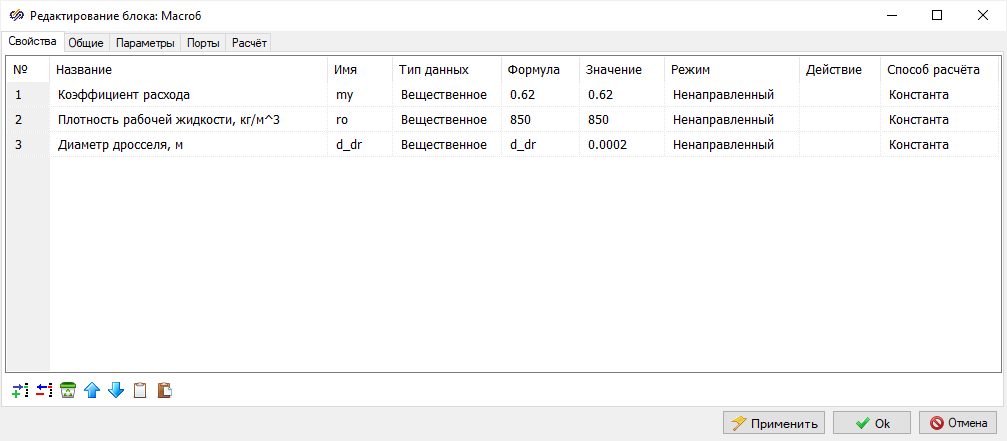
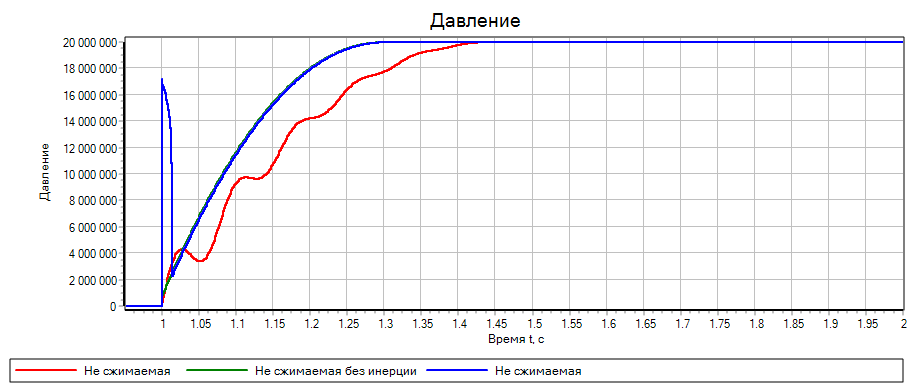
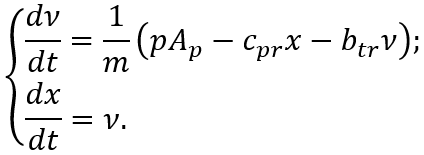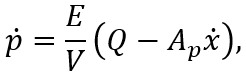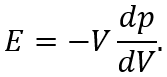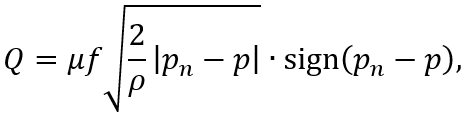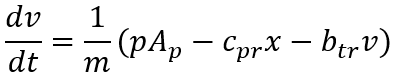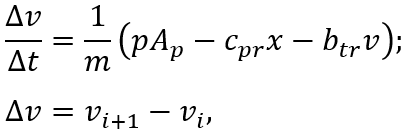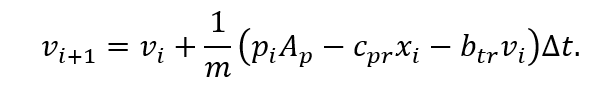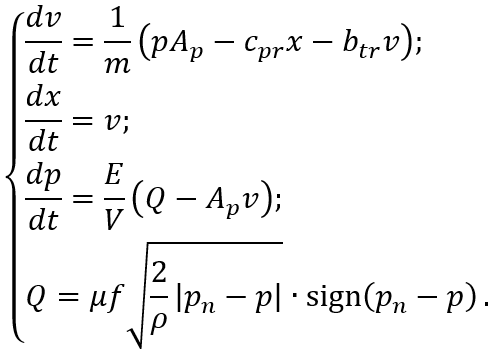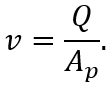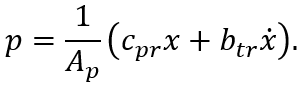Блок диаграмма математической модели при различных допущениях
При написании математической модели необходимо учитывать насколько подробно
необходимо описать каждый элемент системы.
В данной лабораторной работе в модели плунжера возможно использование поршня, а
вместо пружины - упругого элемента. Плунжер возможно представить как весомый или
невесомый. Жидкость возможно моделировать как сжимаемую или несжимаемую. Объем
камеры возможно считать изменяемым или постоянным. Дроссель возможно
моделировать с учетом трубы, в которую он встроен, или без ее учета. Комбинация
этих факторов дает как минимум 8 вариантов математической модели представленной
схемы.
Если подробно остановиться на двух факторах: учет массы плунжера и сжимаемость
жидкости, то тогда также нужно учесть и гравитацию Луны, и силу ветра в
помещении. Однако, на практике инерция и сжимаемость жидкости не всегда
оказывают значительное влияние на процесс перемещения плунжера. Например, при
применении силы более 150 кГс и отсутствии пружины, учет массы плунжера
необходим только в том случае, если она сравнима с этой силой. Учет массы в 100
г усложнит расчеты, но не повысит точность. То же самое относится и к давлению в
системе, если оно не превышает 2–5 бар.
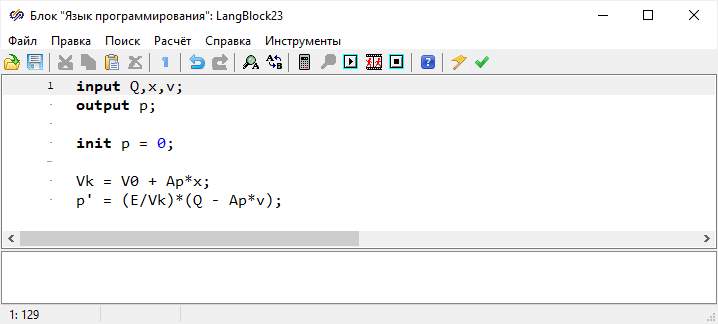
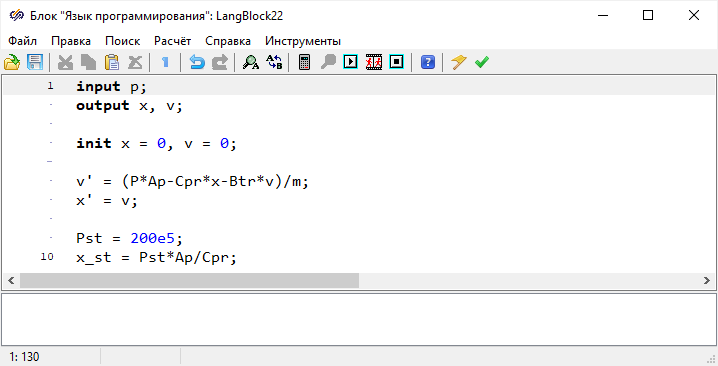
Теперь требуется представить математическую модель плунжера при различных
допущениях. Исходная система уравнений с учетом сжимаемости жидкости выглядит
следующим образом:
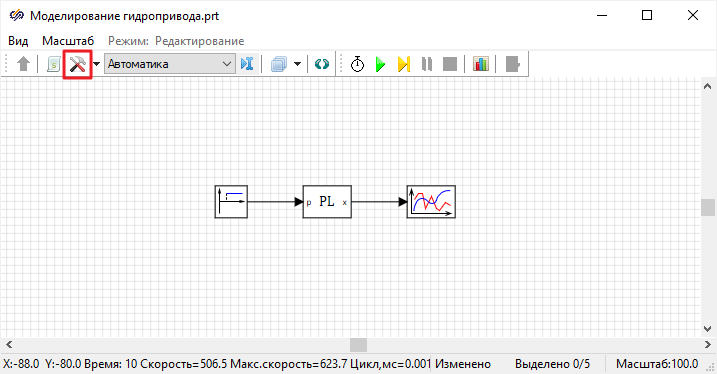
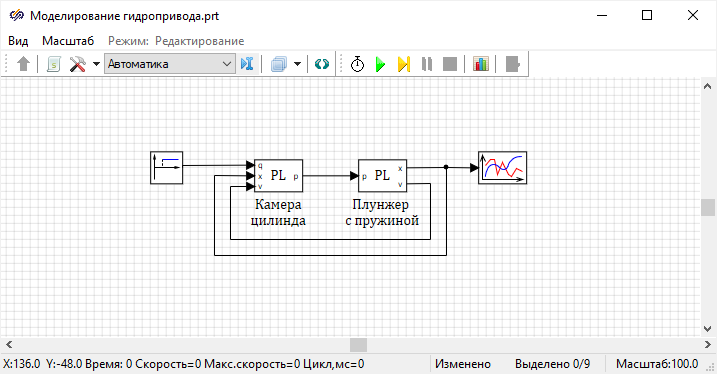
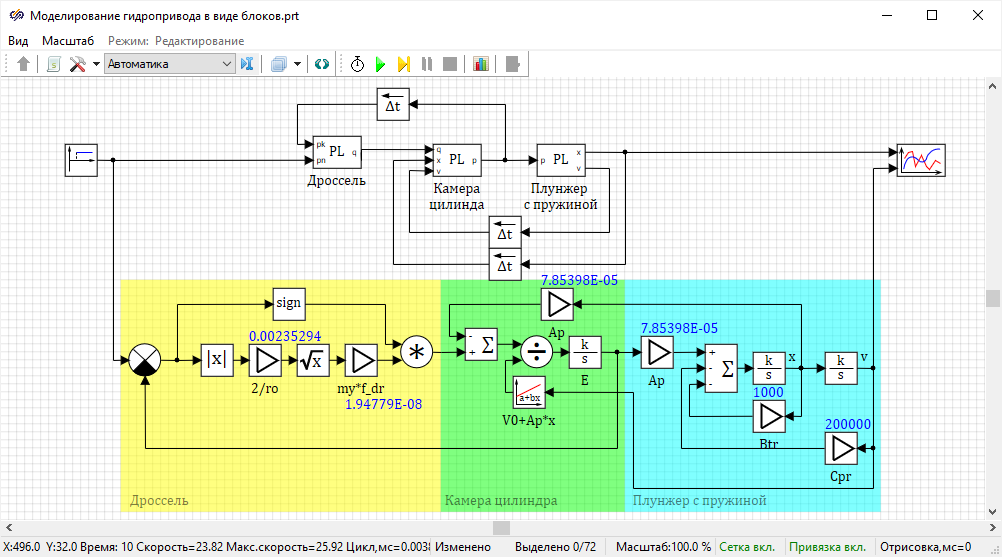
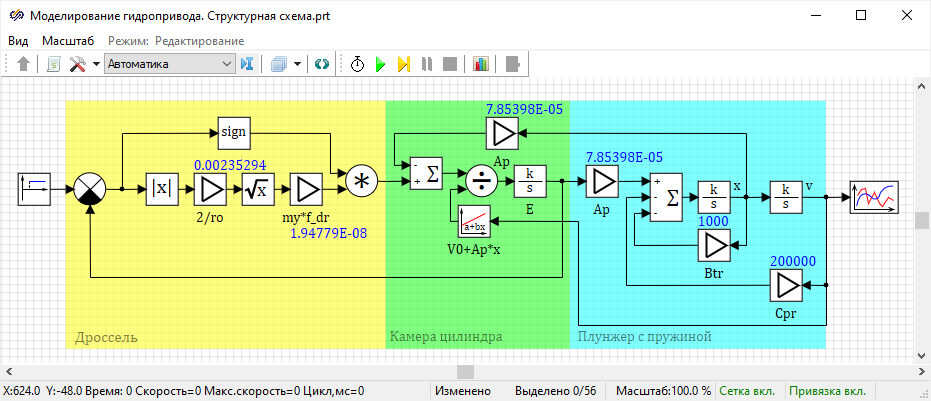
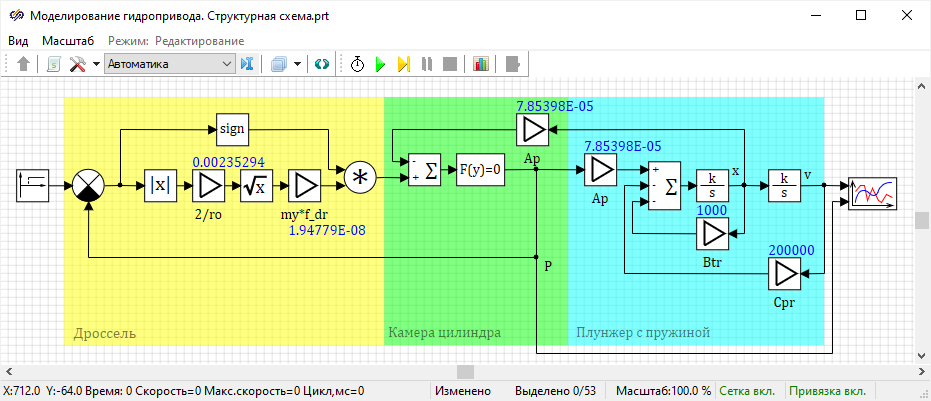
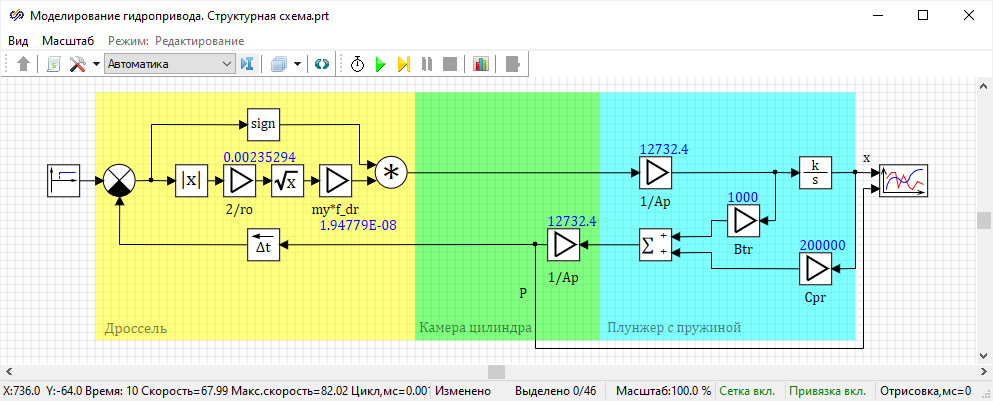
Структурная схема:
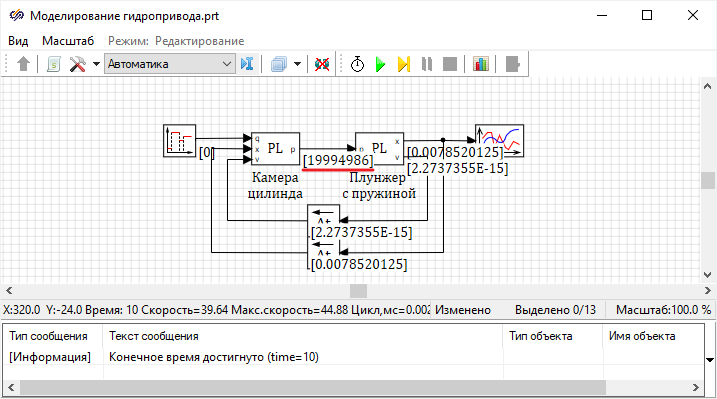
Рисунок 46. Структурная схема
В разработанную раннее
модель необходимо внести изменения, поскольку
необходимо рассмотреть не только перемещение
X, но и давление жидкости
P в рабочей камере. Ведь эффект сжимаемости проявляется не в
мгновенном росте давления. Для этого необходимо открыть модель гидроцилиндра и
добавить в блок «
Порт выхода» еще один выходной сигнал
P и
соединить блоки линиями связи согласно рисунку (
Рисунок 47)
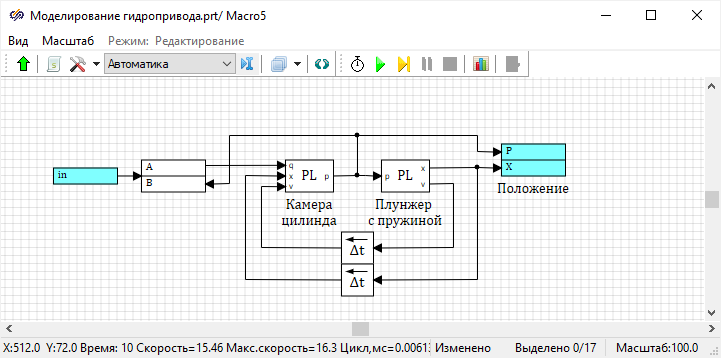
Рисунок 47. Модель гидроцилиндра с добавленным выходным сигналом P
Добавить еще один входной порт для блока «
Временной график», соединить
выходной сигнал блока «
Субмодель» с подписью «
Гидроцилиндр» с
появившемся входным портом блока «
Временной график». Запустить проект на
моделирование. Дождаться окончания процесса моделирования. Открыть результаты
моделирования, которые находятся в блоке «
Временной график» открыть
свойства графика и установить следующие значения на вкладке «
Графики и
оси»:
- Для оси X для графика «График 2» и «График»:
- «Минимум» - «0.9».
- «Максимум» - «2».
- «Шаг сетки» - «0.1».
- «Автомасштаб» - деактивирован.
- Для оси Y для графика «График 2»:
- «Максимум» - «0.01».
- «Автомасштаб» - деактивирован.
- Графики:
- Название графика «График 2» - «Перемещение».
- Название графика «График» - «Давление».
Закрыть окно свойств графика и открыть контекстное меню окна «
График»,
активировать многошкальный режим и разделить шкалы по высоте. Результаты
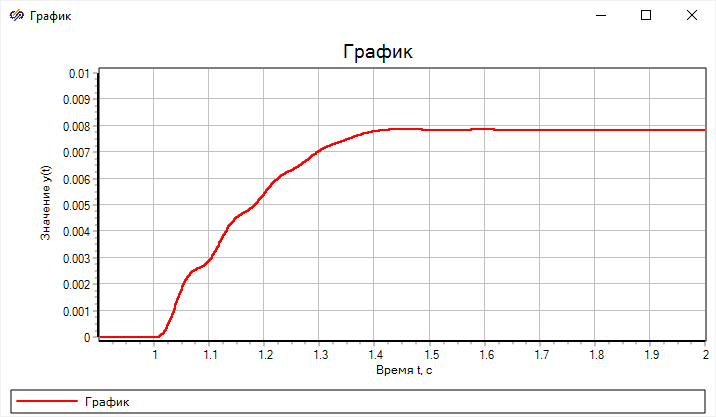
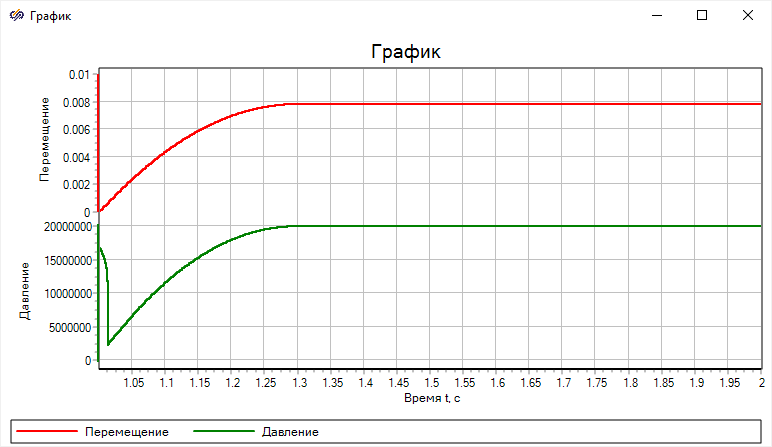
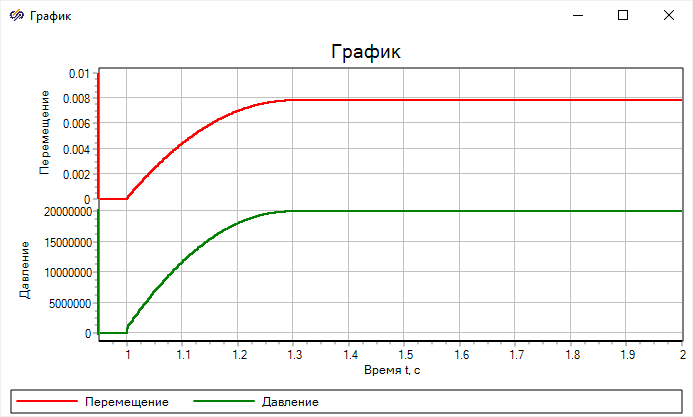
моделирования должны совпадать с результатами на рисунке (
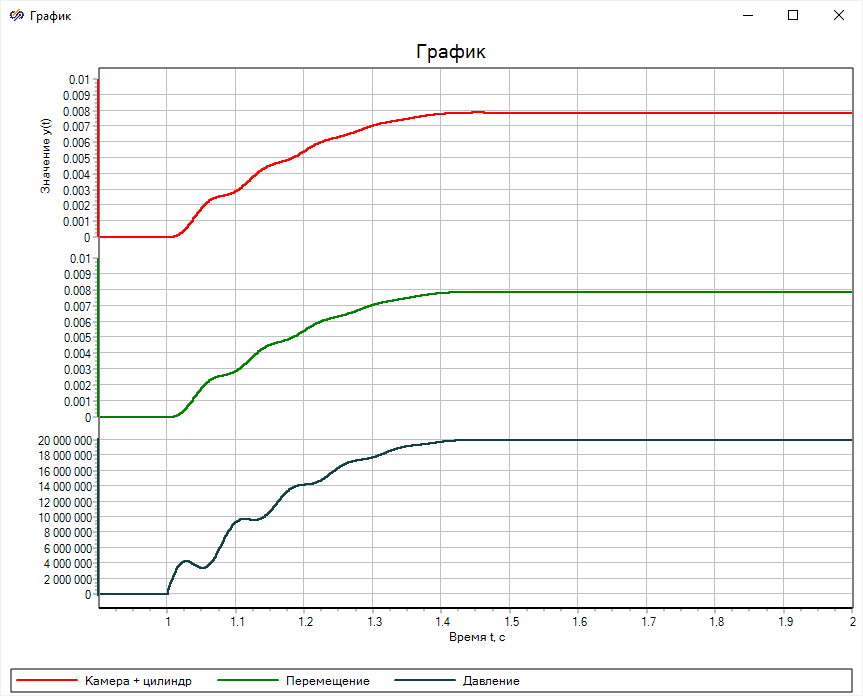
Рисунок 48)
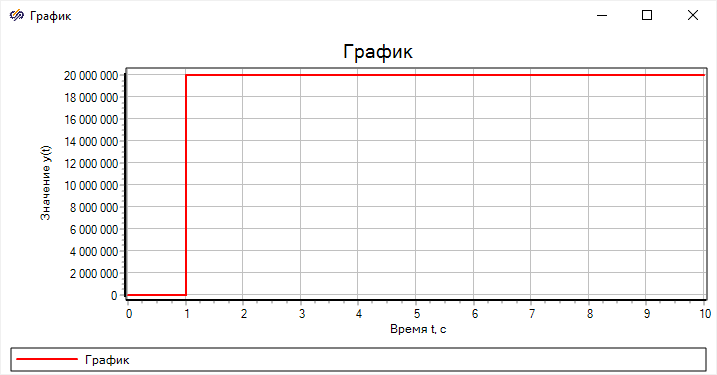
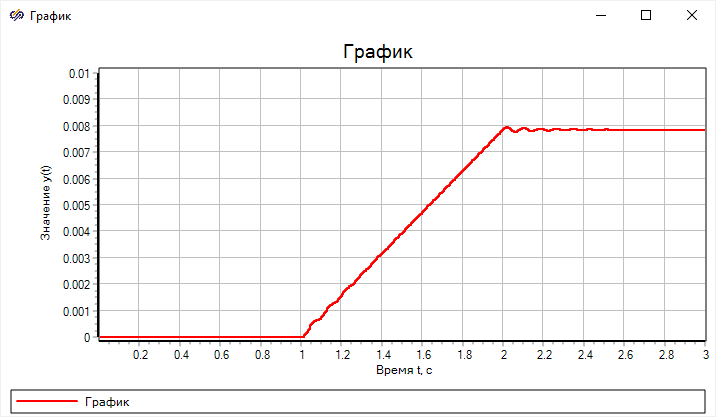
Рисунок 48. Результат переходного процесса плунжера
Перед тем как переходить к моделям с другими допущениями, необходимо
предположить, что жидкость в системе сжимается, то несильно. Тогда давление
рассчитывается исходя из равенства расходов:
Теоретически, в уравнение возможно подставить уравнение расхода через дроссель,
перенести геометрический расход вправо и возвести все в квадрат, поскольку в
системе присутствует всего два расхода. Таким образом, получится уравнение,
которое позволяет определить давление через скорость поршня. Если бы в был еще
один дроссель (например, на сливе), то требовалось бы возводить в квадрат
дважды, при трех дросселях — трижды и так далее. Таким образом, если в
дальнейшем постоянно выражать давление через расход, то в конечном итоге есть
возможность столкнуться с невозможностью найти аналитическое решение для
подобной задачи. Поэтому даже этот простой пример в SimInTech будет
рассчитываться численно.
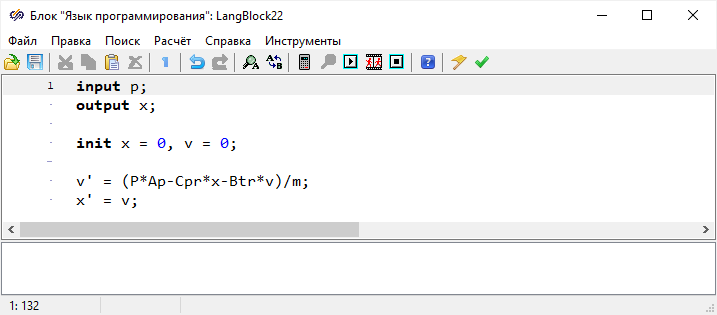
Таким образом, вместо блока «
Интегратор» с подписью «
E», который
определяет давление путем интегрирования, требуется установить блок
«
Нелинейное уравнение F(y) = 0» из вкладки «
Операторы» для
численного решения алгебраических уравнений. Работа блока заключается в
использовании численного итерационного метода для постепенного изменения
выходного значения, пока не будет достигнуто нулевое значение функции с заданной
точностью. Иными словами, на каждом шаге решения блок будет изменять давление,
пока сумма расходов не станет равной нулю с заданной точностью. Тогда
структурная схема будет выглядеть так, как показано на рисунке (
Рисунок 49):
Рисунок 49. Схема расчета без учета сжимаемости
Поскольку до 1 секунды процесса сигналы равны 0, то свойство «
Начальное
приближение» блока «
Нелинейное уравнение F(y) = 0»
устанавливается равным 0. Перед запуском проекта на моделирование необходимо
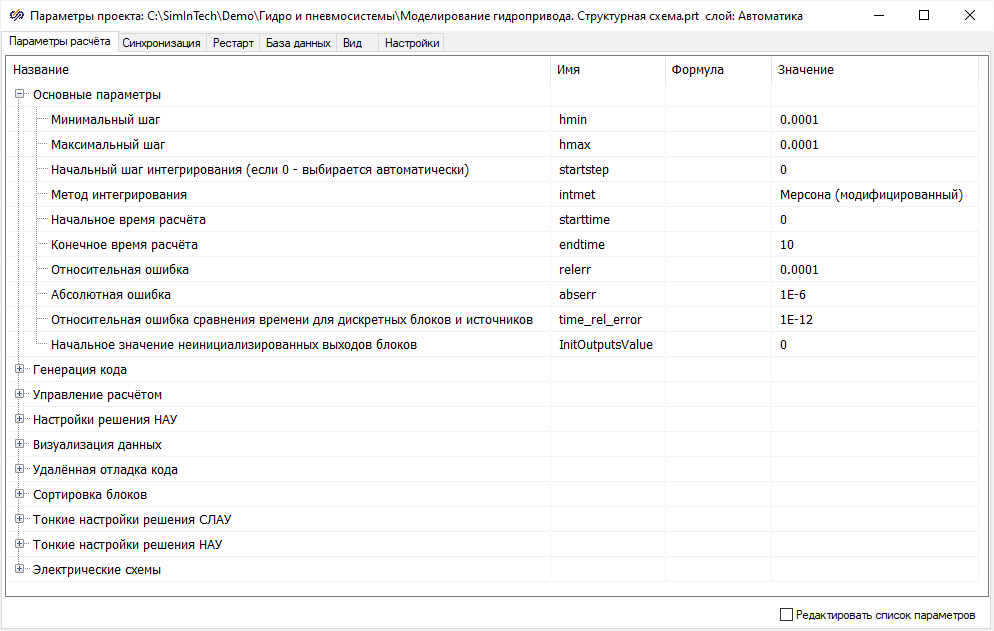
настроить параметры проекта. Требуется установить параметр
«Метод
интегрирования» равным «
Мерсона (модифицированный)», который был
установлен эмпирическим путем.
Рисунок 50. Окно параметров расчета проекта
Если запустить проект на моделирование, то получатся следующие результаты (
Рисунок 51), при этом в окне
сообщений появятся три предупреждения, что заданная точность не
обеспечивается.
Рисунок 51. Результат моделирования без учета сжимаемости
Из результатов видно, что колебания, которые были связаны не только с инерцией
плунжера, но и со сжимаемостью жидкости, исчезли. Однако, на 1 секундах расчета
давление резко возросло до 200 бар, затем постепенно увеличилось до 200 бар.
Такое давление должен компенсировать установленный дроссель, однако блок
«Нелинейное уравнение F(y) = 0» определил, что в момент резкого
возрастания давление в камере должно быть равно давлению нагнетания, а затем оно
уменьшается сразу после начала движения поршня.
Если не учитывать влияние инерции, то скорость перемещения поршня v будет
полностью определяться расходом, поступающим в полость:
Для расчета расхода через дроссель, необходимо знать давление p в полости,
которое рассчитывается из уравнения равновесия:
Таким образом, необходимо удалить следующие блоки:
- блок «Сумматор» с тремя входами;
- блок «Нелинейное уравнение F(y) = 0»;
- блок «Интегратор»;
И разместить блок «
Задержка на шаг интегрирования» из вкладки
«
Нелинейные» для развязки алгебраической петли. Для блоков
«
Усилитель», размещенных в группе «
Камера цилиндра» и
«
Плунжер с пружиной», с подписями «
Ap» установить свойство
«
Коэффициент усиления» равным «
1/Ap». Блок «
Сумматор»
необходимо зеркально отразить с помощью контекстного меню кнопки «
Зеркальное
отражение» и изменить значение свойства «
Весовые множители для
каждого из входов» на «
[1 , 1]», а порты блока «
Задержка на
шаг интегрирования» повернуть на 180 градусов. Разместить и соединить
блоки линиями связи согласно рисунку (
Рисунок 52)
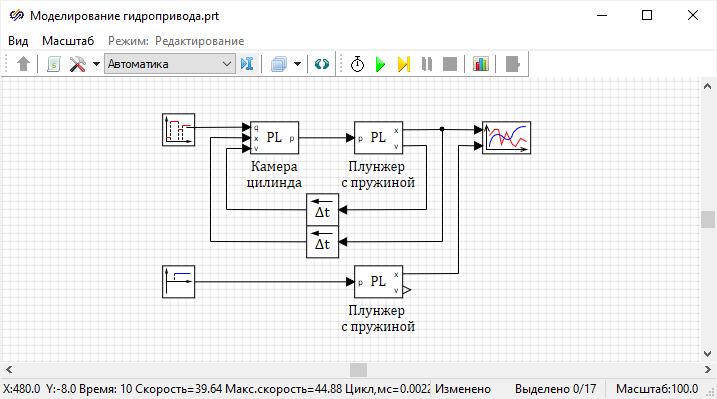
Рисунок 52. Структурная схема без сжимаемости и инерции
Перед запуском проекта на моделирование необходимо настроить параметры проекта.
Требуется установить параметр
«Метод интегрирования» равным
«
Эйлера», для увеличения скорости расчета. Запустить проект на
моделирование. Дождаться окончания процесса моделирования. Открыть результаты
моделирования, которые находятся в блоке «
Временной график» открыть
свойства графика и установить следующие значения на вкладке «
Графики и
оси»:
- Для оси X:
- «Минимум» - «0.95».
- «Максимум» - «2».
- «Автомасштаб» - деактивирован.
- Для оси Y:
- «Максимум» - «0.01».
- «Автомасштаб» - деактивирован.
Закрыть окно свойств графика и открыть контекстное меню окна «
График»,
активировать многошкальный режим и разделить шкалы по высоте. Результаты
моделирования должны совпадать с результатами на рисунке (
Рисунок 53)
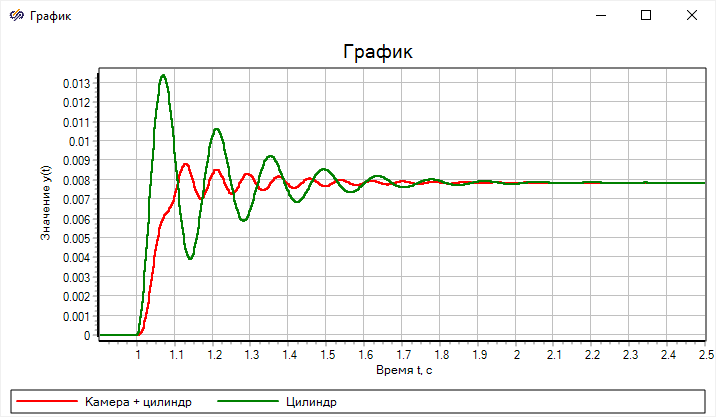
Рисунок 53. Результат моделирования без учета инерции и сжимаемости
Теперь практически отсутствует скачок давления в начальный момент времени
переходного процесса (при t = 1 с), хотя давление не начинается с нуля. Это
объясняется тем, что в начальный момент времени из-за перепада давления в
системе сразу же возникает расход через дроссель. Следовательно, скорость в
начальный момент времени также не равна нулю, что приводит к появлению ненулевой
силы вязкого трения в уравнении равновесия. В результате возникает небольшой
скачок давления в начале переходного процесса.
Результаты сравнения моделирования при разных допущениях:
Если сравнить
вычислительную трудоемкость расчетов при разных допущениях, то показатели
следующие:
| Параметр |
С учетом сжимаемости и
инерции |
Без учета
сжимаемости |
Без учета сжимаемости и
инерции |
| Метод
интегрирования |
Эйлера |
Эйлера |
Мерсона
(модифицированный) |
| Минимальный
шаг |
0.0001 |
0.0001 |
0.0001 |
| Максимальный
шаг |
0.0001 |
0.0001 |
0.0001 |
| Максимально возможное
ускорение |
9,712 раз |
39.89 раз |
3.677 раз |
| Число шагов |
100000 |
100000 |
100000 |
Таким образом, в задаче необходимо учитывать сжимаемость рабочей жидкости, так
как колебания системы связаны именно с этим свойством. В моделях, в которых
учитывается только инерция, но не сжимаемость не оправдались. Видно, что при
таких допущениях решатель выдает «рваный» график давления, что может быть
связано с разными порядками расходов (1e-3) и давлений (1e+6). Кроме того, это
приводит к большей вычислительной трудоемкости, даже без учета внутренних
итераций.
Невозможно однозначно рекомендовать, в каких случаях нужно учитывать сжимаемость
жидкости, а в каких - нет. Постоянная времени сжимаемого объема жидкости зависит
от многих факторов. Общая рекомендация состоит в том, чтобы лучше учитывать
сжимаемость везде, хотя это может увеличить время расчета. Однако, если
известно, что масса пренебрежимо мала, то можно не учитывать ни сжимаемость, ни
инерцию, что позволит упростить систему дифференциальных уравнений для каждого
элемента на два порядка. В остальных случаях следует разрабатывать несколько
математических моделей с различными допущениями и выбирать наиболее подходящую
на основе фактических данных.
Использование библиотеки готовых элементов
Разработка математических моделей для разных допущений, а также разработка
соответствующей структурной схемы в разы увеличивает время. Для упрощения задачи
многие производители программ CAE улучшают пользовательский интерфейс, где
математическая модель разрабатывается подобно сборке физической системы, а также
используются готовые блоки физических элементов, что значительно облегчает
процесс.
Разработка моделей собственными блоками в SimInTech, по известным уравнениям было
рассмотрено в разделе (Разработка принципиальной схемы модели). Теперь
требуется разработать модель из уже готовых блоков в SimInTech. В SimInTech есть
библиотека «Гидро- и пневмосистемы», которая постоянно дорабатывается и
расширяется. В ней уже содержатся готовые элементы, в которых подготовлены порты
для соединения элементов в принципиальные гидравлические схемы. В SimInTech есть
так же библиотека «Механика», где содержатся элементы для моделирования
механических систем.
Требуется создать новый проект и разместить в нем следующие блоки:
- Из библиотеки «Гидро- и пневмосистемы»:
- 1 блок «ГПС - Давление и температура жидкости» из
подгруппы «Граничные условия».
- 1 блок «ГПС - Гидравлический турбулентный дроссель
постоянного сечения» из подгруппы «Дроссельные
элементы».
- 1 блок «ГПС - Гидравлическая полость переменного объема»
из подгруппы «Полости».
- 1 блок «ГПС - Гидромеханический преобразователь
поступательного типа» из подгруппы «Гидро- и
пневмомеханические преобразователи».
- Из библиотеки «Механика» из подгруппы «Элементы
поступательного движения»:
- 1 блок «Механика - Инерция поступательного
движения».
- 1 блок «Механика - Фрикционный демпфер поступательного
движения».
- 1 блок «Механика - Пружина поступательного
движения».
- 1 блок «Механика - Заделка поступательного
движения».
- 1 блок «Ступенька» из вкладки «Источники».
- 1 блок «Запись в список сигналов» из вкладки
«Сигналы».
Зеркально отразить блоки «
ГПС - Гидравлическая полость переменного объема»
и «
ГПС - Гидромеханический преобразователь поступательного типа».
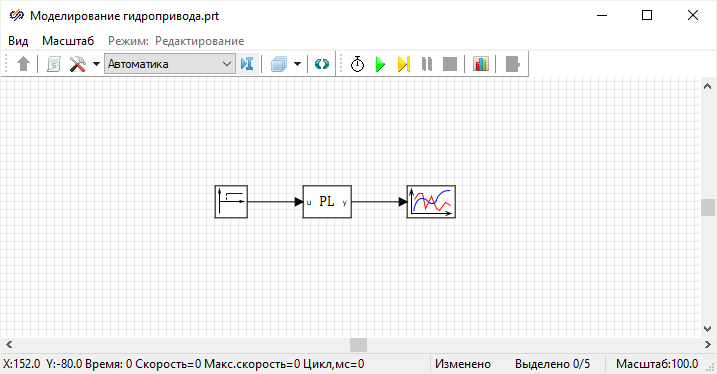
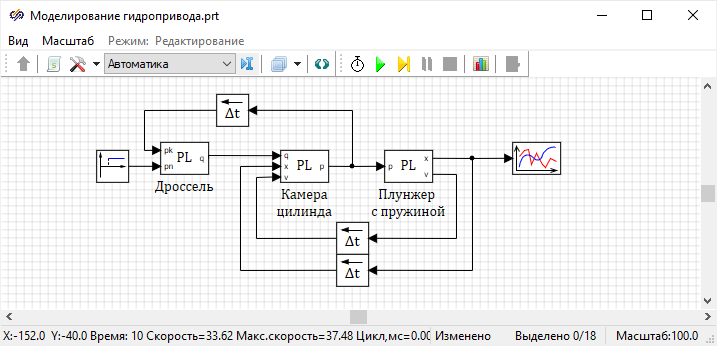
Разместить и соединить блоки линиями связи согласно рисунку (
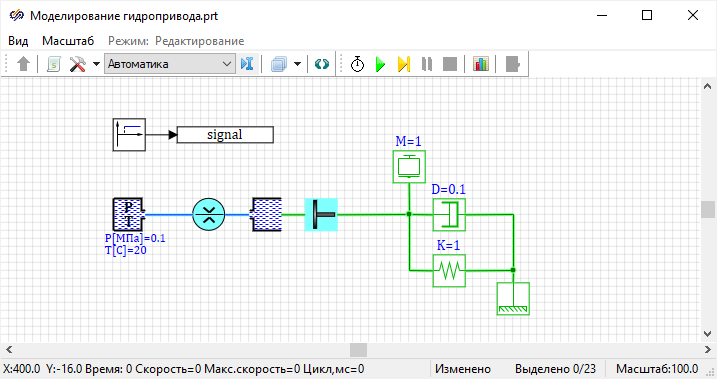
Рисунок 54):
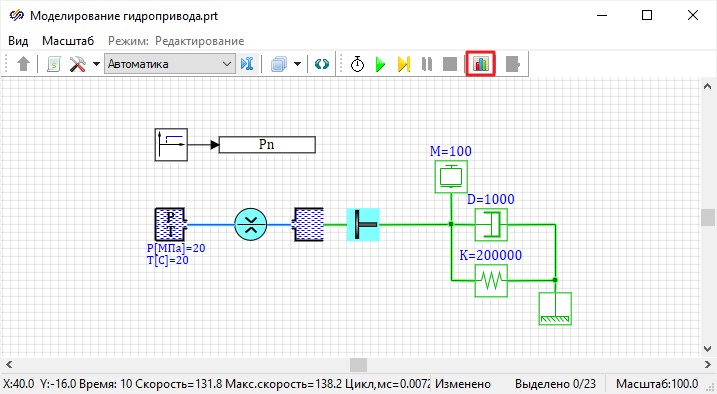
Рисунок 54. Рабочая область проекта с использованием стандартных блоков
Особенностью данной схемы, является то, что изображенные на ней линии
связи имеют различное значение: то есть если соединить полость с пружиной, то
линия связи не будет соединять блоки:
- Линии связи между блоками «ГПС - Давление и температура жидкости»
и «ГПС - Гидравлическая полость переменного объема» – это каналы
течения жидкости.
- Линия связи между блоками «ГПС - Гидромеханический преобразователь
поступательного типа» и «Механика - Заделка поступательного
движения» – это линия механической связи.
- Линия связи между блоками «Ступенька» и «Запись в список
сигналов» – это линия передачи данных (одного сигнала).
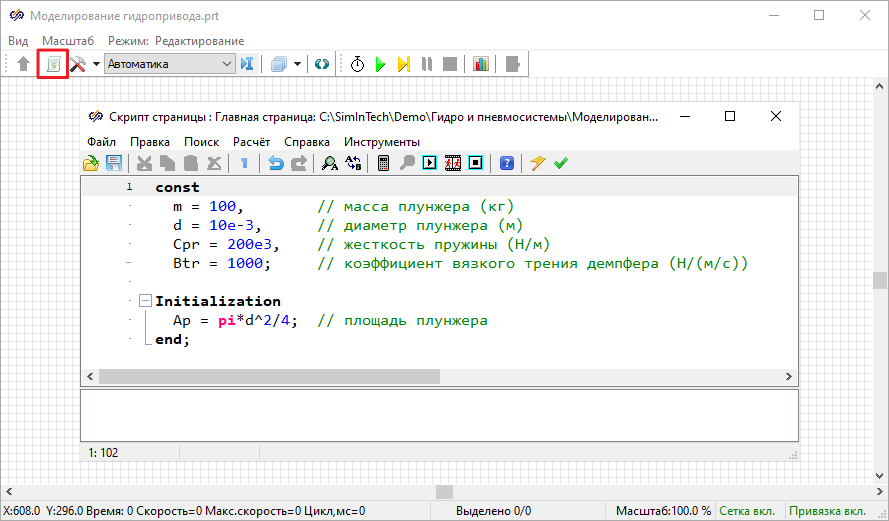
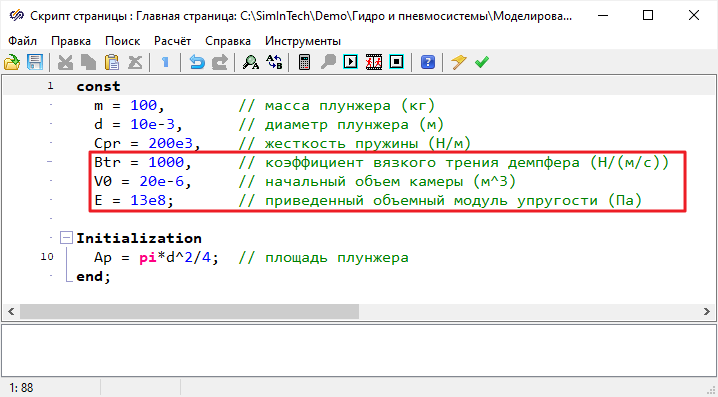
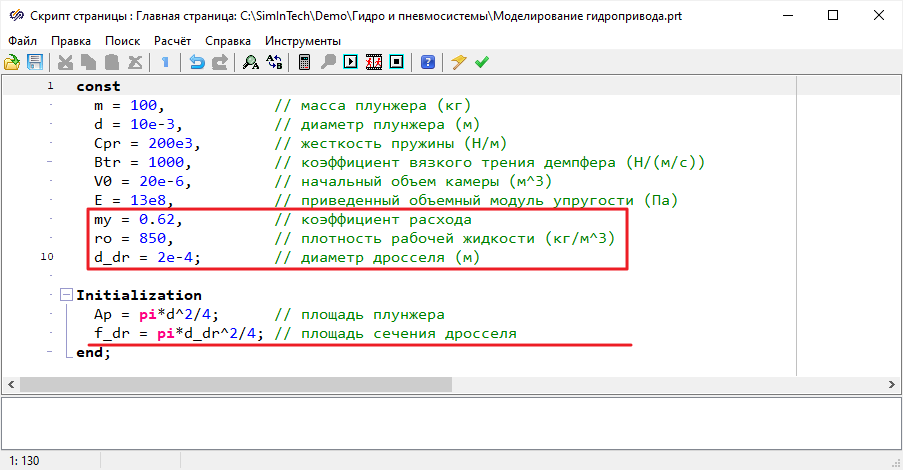
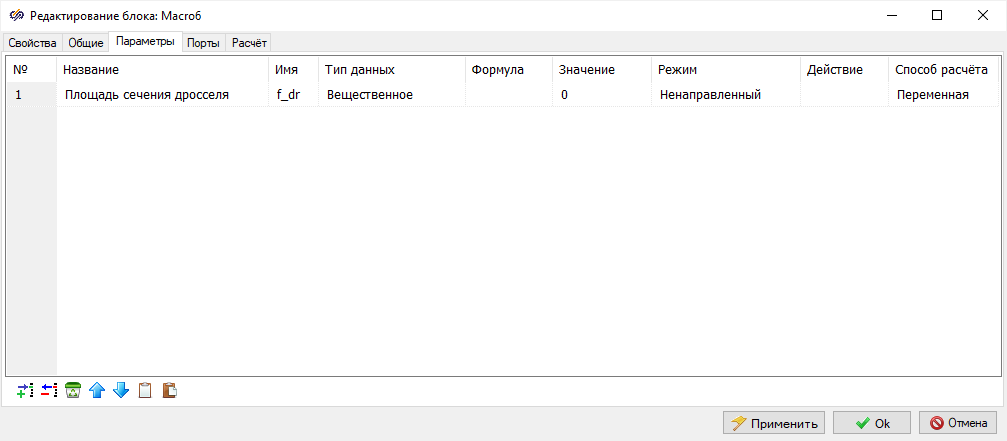
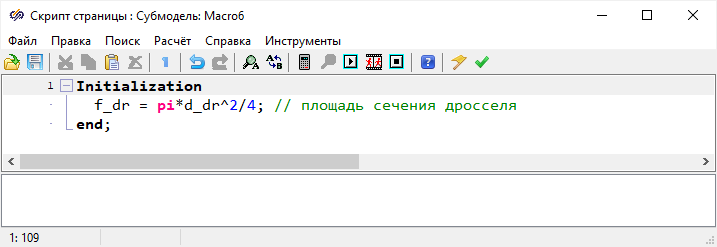
Добавить в скрипт проекта константы и расчет площади плунжера и сечения дросселя,
которые задавали в предыдущих моделях (Рисунок 26).
Поскольку блок «
ГПС - Давление и температура жидкости» не имеет входных
портов, на который нужно подать ступенчатый сигнал от блока «
Ступенька»
для имитации скачка давления, поэтому необходим блок «
Запись в список
сигналов», который будет принимать сигнал от блока «
Ступенька» и
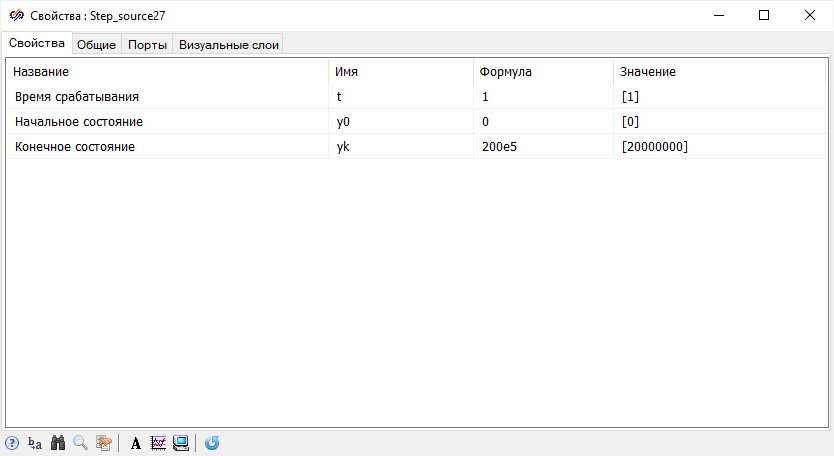
передавать в сигналы проекта. Для начало создадим ступенчаты сигнал в блоке
«
Ступенька», для этого необходимо задать следующие свойства:
- «Время срабатывания» - «1».
- «Начальное состояние» - «0».
- «Конечное состояние» - «200e5».
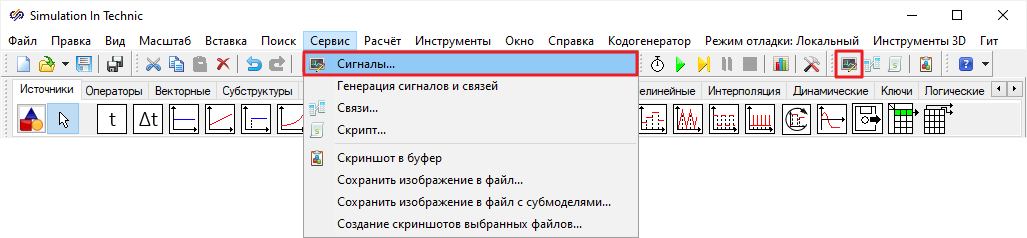
После задания ступенчатого сигнала необходимо создать сигнал, который будет
принимать скачок давления. Для этого необходимо в главном окне SimInTech нажать
на кнопку «
Сигналы», которая выделена на рисунке (
Рисунок 55) или нажать на
меню «
Сервис» в открывшемся списке выбрать «
Сигналы».
Рисунок 55. Главное окно SimInTech c выделенными кнопками «Сигналы»
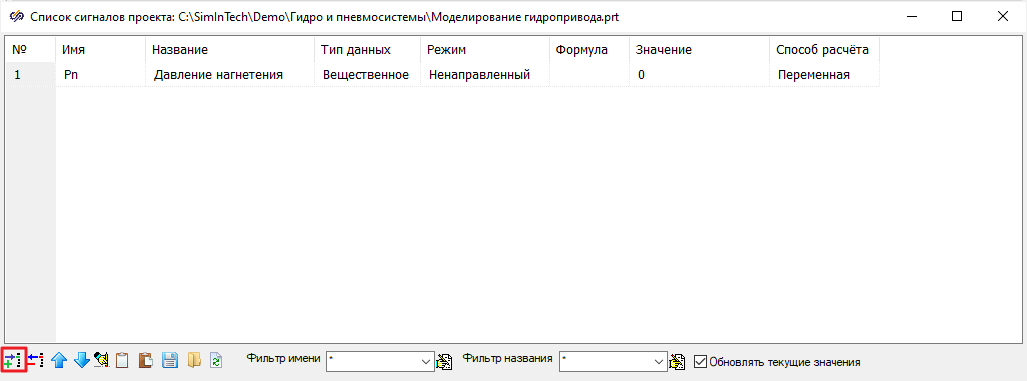
В открывшемся окне «
Список сигналов проекта» добавить при помощи кнопки
«
Добавить сигнал» новый сигнал и задать ему параметры согласно
рисунку (
Рисунок 56).
Рисунок 56. Добавление нового сигнала в список сигналов проекта
Теперь необходимо установить привязку выходного сигнал блока «
Ступенька» к
созданному сигналу «
Pn», для этого необходимо открыть свойства блока
«
Запись в список сигналов» и в строке свойства «
Имена
сигналов» задать в поле «
Значение» значение «
Pn». Теперь в
окне проекта блок «
Запись в список сигналов» отображает «
Pn».
Теперь сигнал «
Pn» записывает значение выходного сигнала блока
«
Ступенька». Назначить для блока «
ГПС - Давление и температура
жидкости» входной сигнал «
Pn», а также задать следующие
свойства:
- «Абсолютное давление рабочей среды в полости, Па» -
«Pn».
- «Температура рабочей среды в полости, градусы Цельсия» -
«20».
Для оставшихся блоков также следует задать свойства. Поскольку плотность рабочей
жидкости задать в блоках «ГПС - Гидравлический турбулентный дроссель
постоянного сечения» и «ГПС - Гидравлический турбулентный дроссель
постоянного сечения» нет возможности, то выбирается наиболее близкая
среда АМГ-10, плотность которой равна 835,6 кг/м3.
Для блока «
ГПС - Гидравлический турбулентный дроссель постоянного сечения»
задать следующие свойства:
- «Коэффициент массового расхода дросселя при прямом токе рабочей
среды» - «my» = «0.62».
- «Коэффициент массового расхода дросселя при обратном токе рабочей
среды» - «my» = «0.62».
- «Диаметр дросселя при прямом токе рабочей среды, м» -
«d_dr» = «0.0002».
- «Диаметр дросселя при обратном токе рабочей среды, м» -
«d_dr» = «0.0002».
- «Рабочая среда» - «масло АМГ-10».
Для блока «
ГПС - Гидравлический турбулентный дроссель постоянного сечения»
задать следующие свойства:
- «Начальное абсолютное давление рабочей среды в полости, Па» -
«200e5».
- «Температура рабочей среды в полости, градусы Цельсия» -
«20».
- «Начальный объем полости, м^3» - «V0» =
«20e-6».
- «Рабочая среда» - «масло АМГ-10».
- «Модуль объемной упругости рабочей среды» -
«адиабатный».
- «Нижнее ограничение по абсолютному давлению рабочей среды в полости,
Па» - «0.001e6».
- «Верхнее ограничение по абсолютному давлению, Па» -
«200e6».
Для блока «
ГПС - Гидромеханический преобразователь поступательного типа»
задать следующие свойства:
- «Площадь механического элемента, на которую действует давление в
полости, м^2» - «Ap».
- «Характер силы давления жидкости» - «движущая».
Для блока «
Механика - Инерция поступательного движения» задать следующие
свойства:
- «Масса, кг» - «m» = «100».
- «Начальная скорость, м/с» - «1».
- «Цвет» - «46848».
Для блока «
Механика - Фрикционный демпфер поступательного движения» задать
следующие свойства:
- «Коэффициент демпфирования, Н·с/м» - «Btr» =
«1000».
- «Цвет» - «46848».
Для блока «
Механика - Пружина поступательного движения» задать следующие
свойства:
- «Коэффициент жесткости, Н/м» - «Cpr» =
«200e3».
- «Начальная деформация, м» - «0».
- «Показывать» - «все».
- «Цвет» - «46848».
Для блока «
Механика - Заделка поступательного движения» задать следующие
свойства:
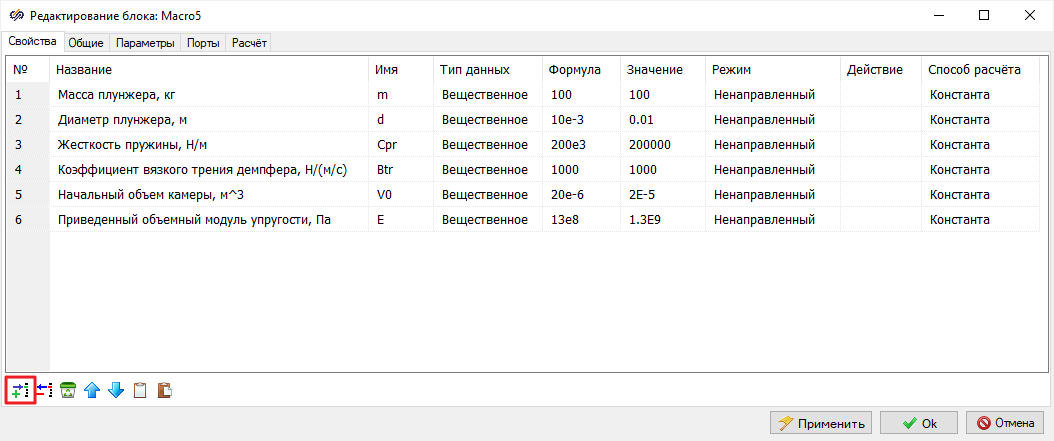
Запустить проект на моделирование и дождаться окончания расчета. В проекте
отобразятся заданные значения (
Рисунок 57).
Рисунок 57. Рабочая область проект со значениями свойств и выделенной кнопкой «Менеджер данных»
Для получения графика сигнала нужного сигнала перемещения пружины, который
рассчитывается в блоке «
Механика - Пружина поступательного движения»
необходимо:
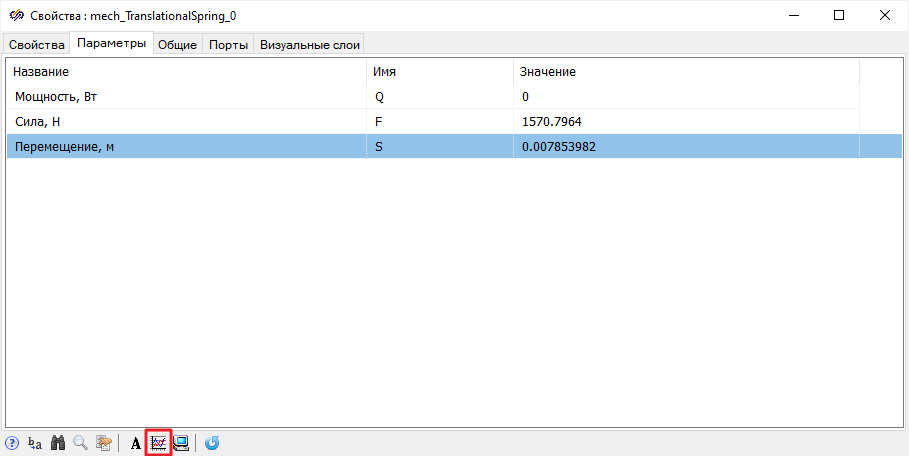
- Открыть окно «Свойства» блока «Механика - Пружина
поступательного движения».
- Перейти на вкладку «Параметры», где перечислены рассчитываемые
величины блока.
- Выбирать параметр «Перемещение, м» и нажать на кнопку «Создать
график» в нижней части окна.
После этого откроется окно «
Перемещение, м (S) в объекте
mech_TranslationalSpring_0», а также в менеджере данных, кнопка вызова
которого выделена на рисунке (
Рисунок 57), отобразится объект «
Графики» с содержимым
««
Перемещение, м (S) в объекте mech_TranslationalSpring_0»».Таким же
образом можно построить график для любых параметров любого блока, а также
перетаскивать на один график переменные из разных блоков.
Рисунок 58. Вызов графиков для стандартных объектов
Запустить проект на моделирование заново, чтобы в окне «
Перемещение, м
(S) в объекте mech_TranslationalSpring_0» построился график. Открыть
свойства графика и установить следующие значения на вкладке «
Графики и
оси»:
- Для оси X:
- «Минимум» - «0.9».
- «Максимум» - «2».
- «Автомасштаб» - деактивирован.
- Для оси Y:
- «Максимум» - «0.01».
- «Автомасштаб» - деактивирован.
- Графики:
- Название графика «Перемещение, м (S) в объекте
mech_TranslationalSpring_0» - «Перемещение».
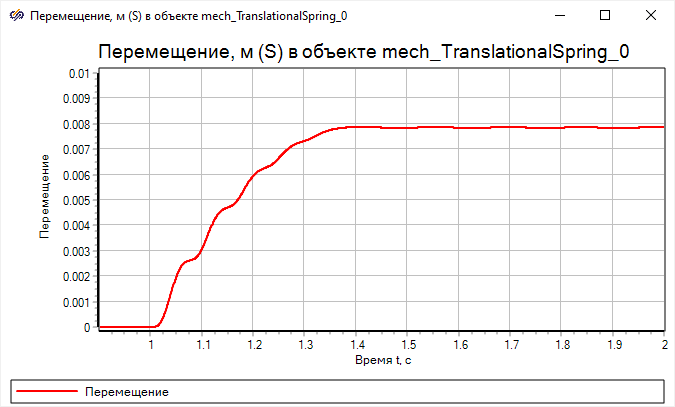
Рисунок 59. Результаты моделирования
Теперь дополним проект моделью гидропривода, построенного ранее при помощи блоков
«
Субмодель», для сравнения расчетов. Также добавить на схему блок
«
Константа», который будет принимать сигнал перемещения пружины с
блока «
Механика - Пружина поступательного движения». Для этого необходимо
в свойствах блока «
Константа» записать формулу
«
mech_TranslationalSpring_0.S» для свойства «
Значение».Запись
«
mech_TranslationalSpring_0.S» означает следующее
«
mech_TranslationalSpring_0» - это уникальное имя блока «
Механика
- Пружина поступательного движения», которая обозначается в свойствах на
вкладке «
Общее» под свойством «
Имя объекта», «
S» - это
параметр блока «
Механика - Пружина поступательного движения», который
отображается в свойствах блока во вкладке «
Параметры» параметра
«
Перемещение, м». Тогда константа во время моделирования будет
принимать значения параметра перемещение пружины. Разместить и соединить блоки
линиями связи согласно рисунку (
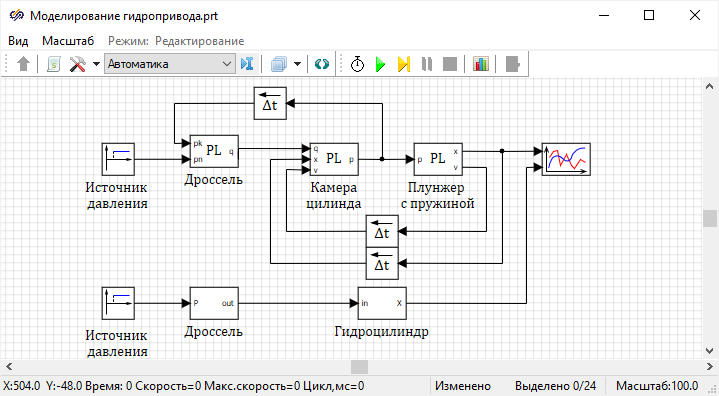
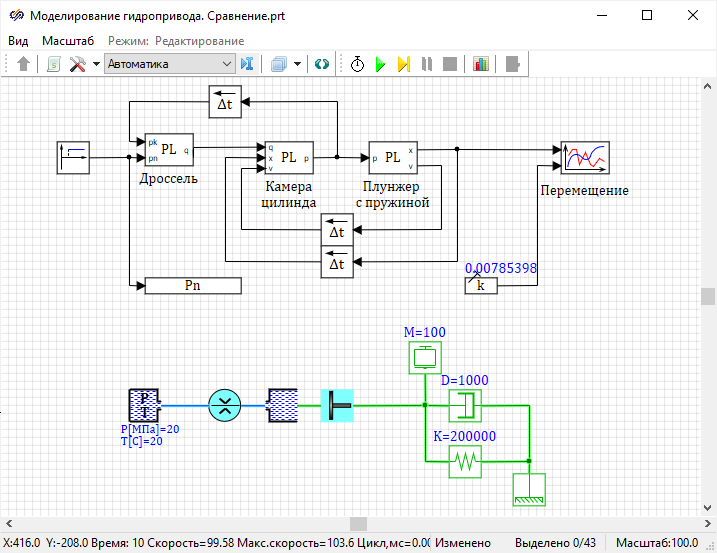
Рисунок 60):
Рисунок 60. Рабочая область проекта с моделью сравнения методов расчета
Запустить проект на моделирование. Дождаться окончания процесса моделирования.
Открыть результаты моделирования, которые находятся в блоке «
Временной
график» открыть свойства графика и установить следующие значения на
вкладке «
Графики и оси»:
- Графики:
- Название графика «Камера + цилиндр» - «Блоки на языке
программирования».
- Название графика «Перемещение» - «Блоки библиотеки
ГПС».
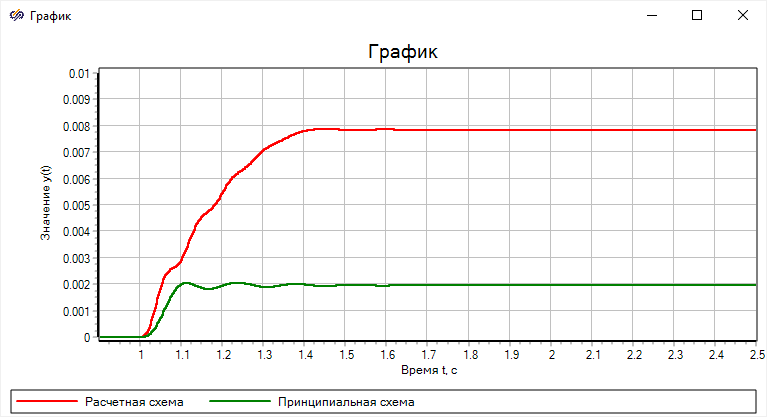
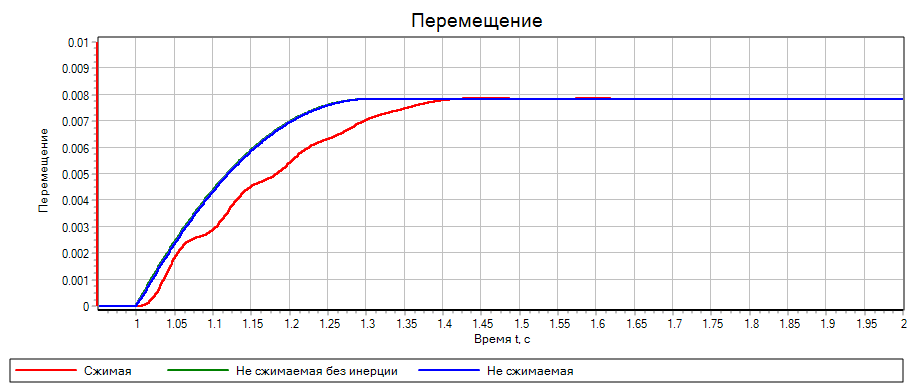
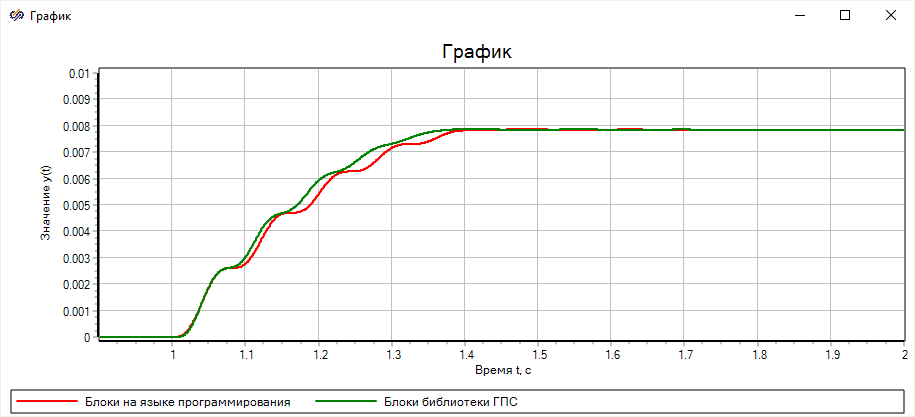
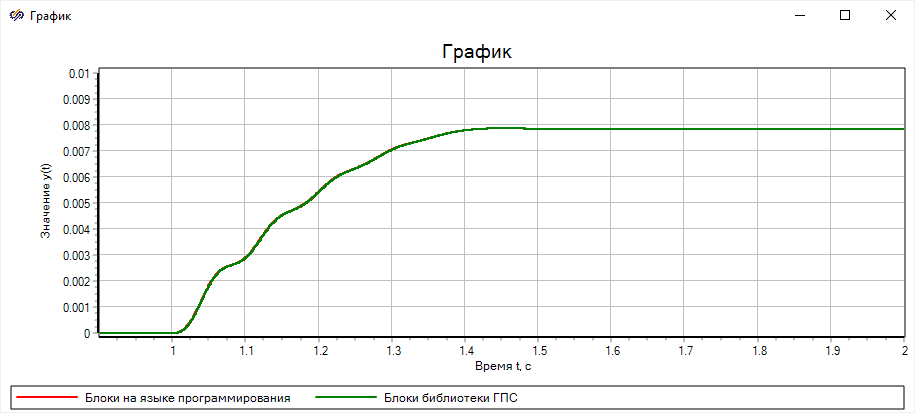
Рисунок 61. Результат сравнения методов
Видно, что значения расходятся в конце переходного процесса. Это связано с
тем, что свойства рабочего тела в стандартной библиотеке берутся из справочника,
тогда как в построенной ранее модели они задавались в виде констант. Однако
данные параметры возможно изменить, если войти в субмодель блока «
ГПС -
Гидравлическая полость переменного объема». Для этого необходимо
выделить блок «
ГПС - Гидравлическая полость переменного объема», открыть
контекстное меню и выбрать пункт «
Действия» в открывшемся списке выбрать
«
Войти в субмодель» (
Рисунок 62).
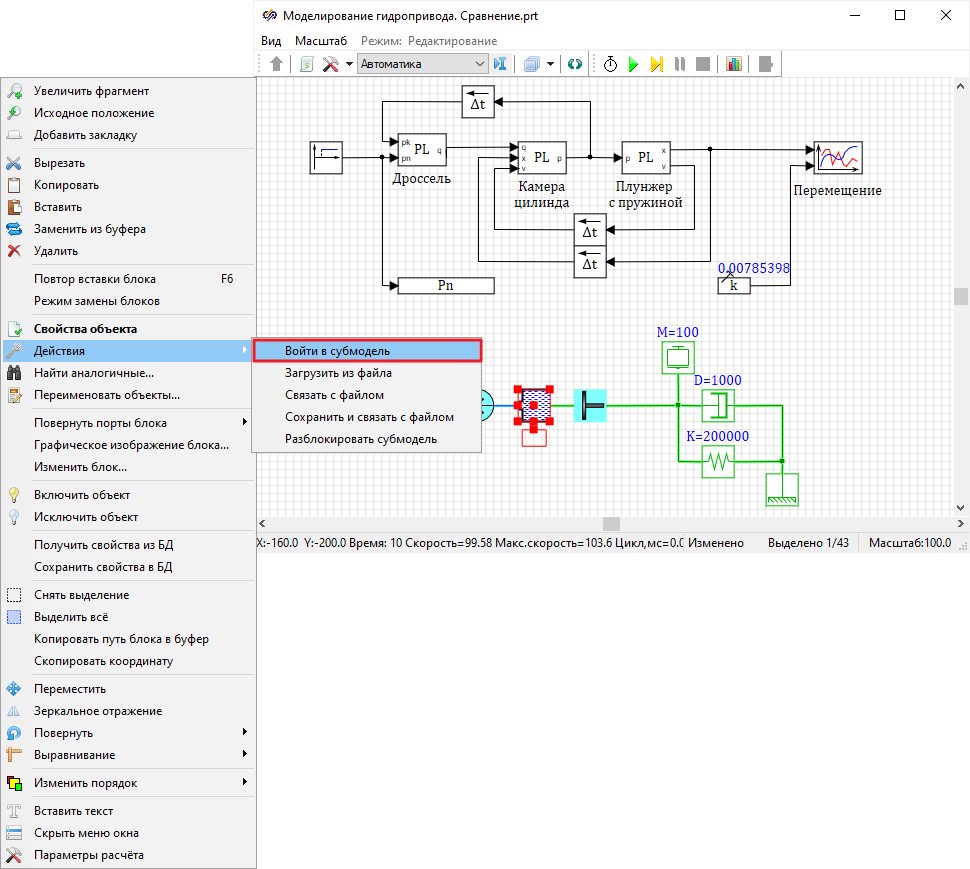
Рисунок 62. Рабочая область проекта с контекстным меню блока «ГПС -
Гидравлическая полость переменного объема»
Откроется рабочая область субмодели блока «
ГПС - Гидравлическая полость
переменного объема»:
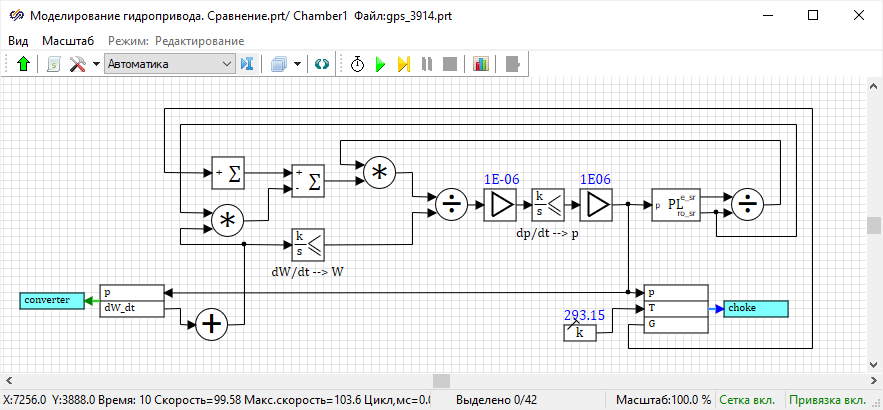
Рисунок 63. Рабочая область субмодели блока «ГПС - Гидравлическая полость
переменного объема»
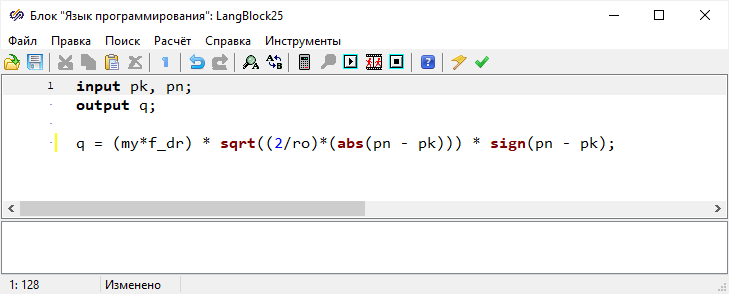
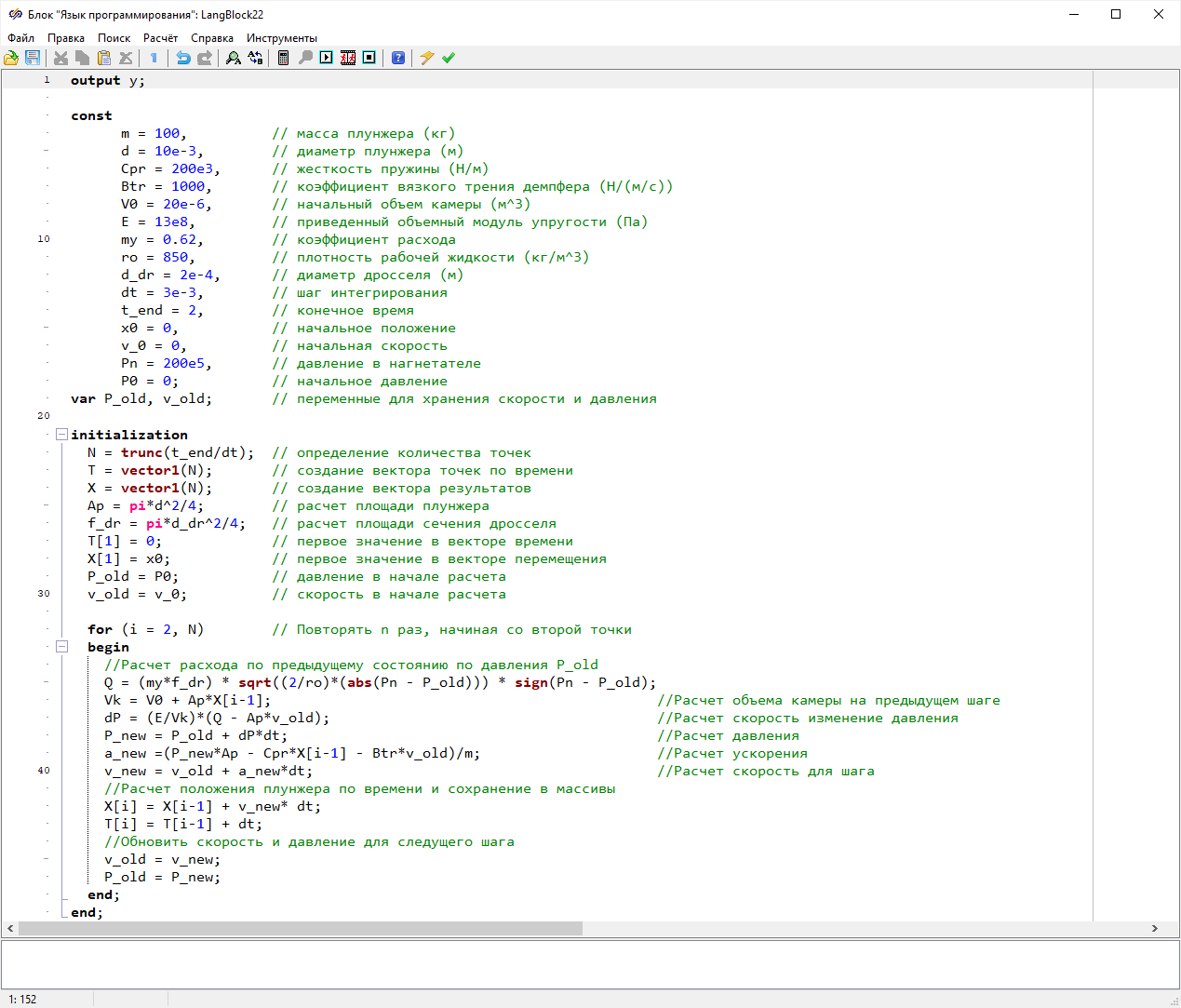
Блок «
Язык программирования» с выходными портами «
e_sr» и
«
ro_sr» отвечает за расчет свойств блока «
ГПС - Гидравлическая
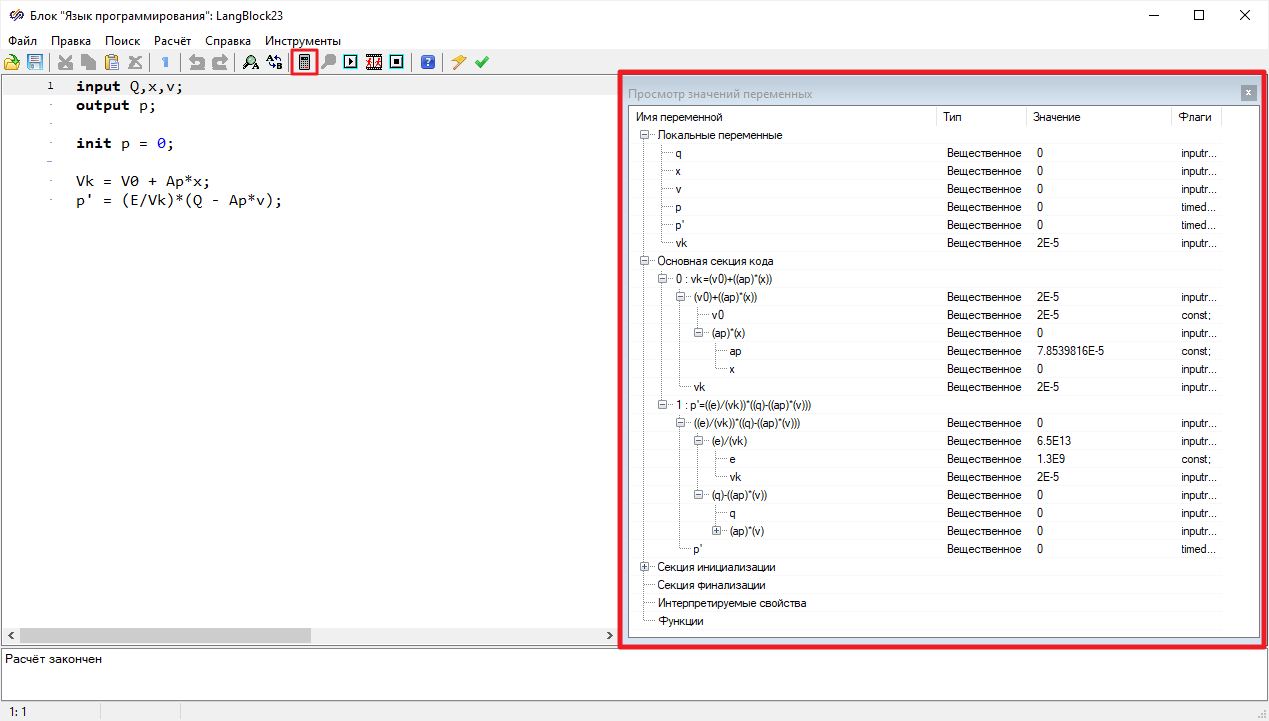
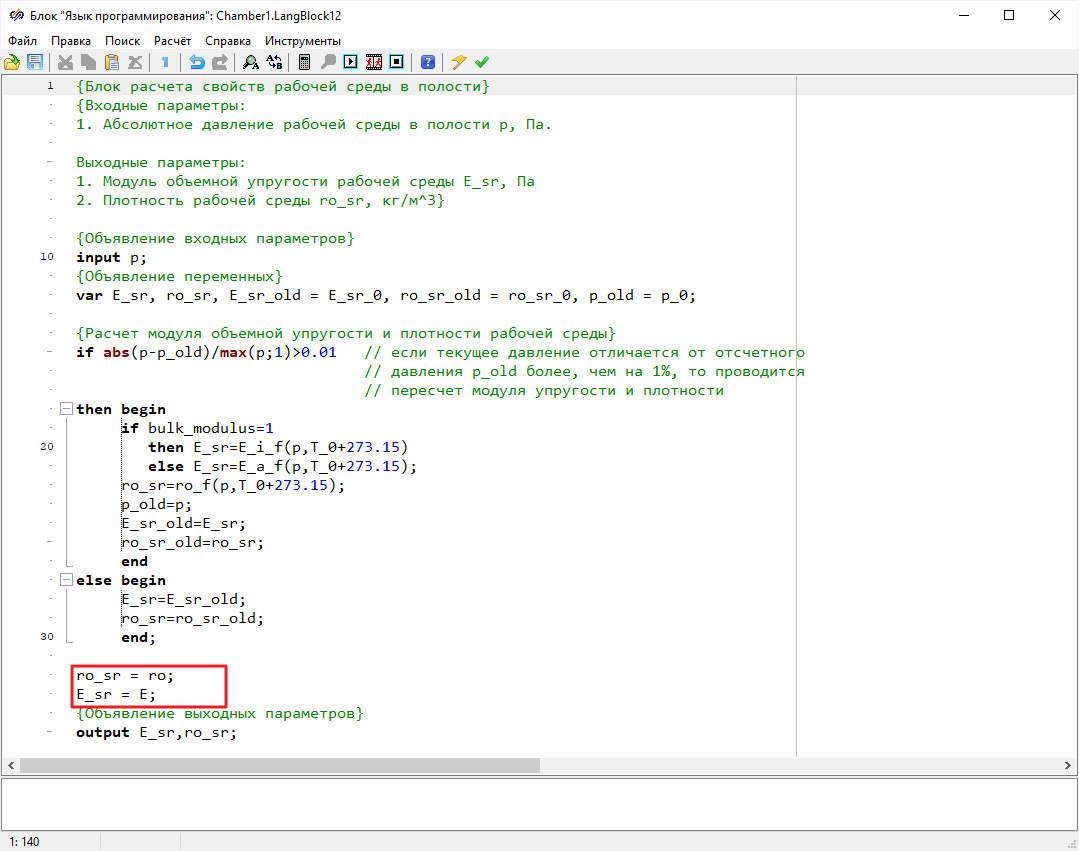
полость переменного объема». Открыть скрипт блока «
Язык
программирования» и добавить вместо расчетных переменных глобальные
константы, заданные в скрипте проекта(
Рисунок 64).
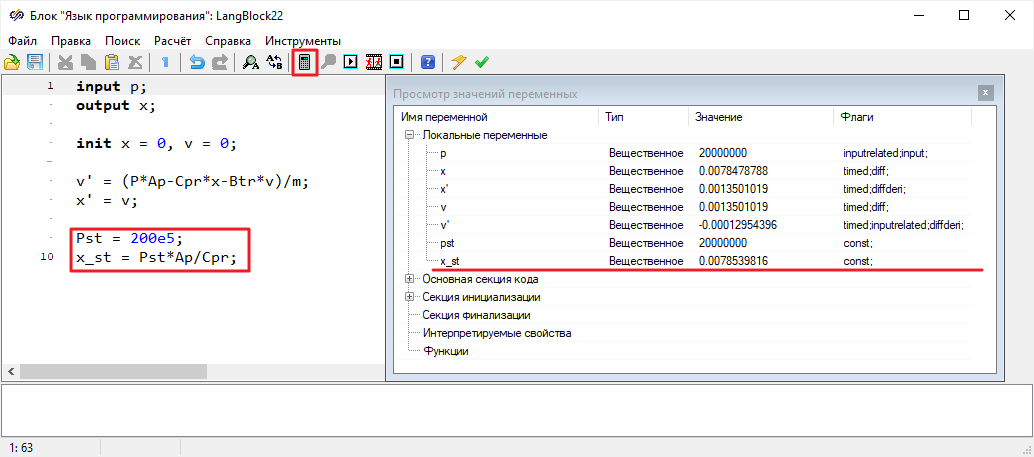
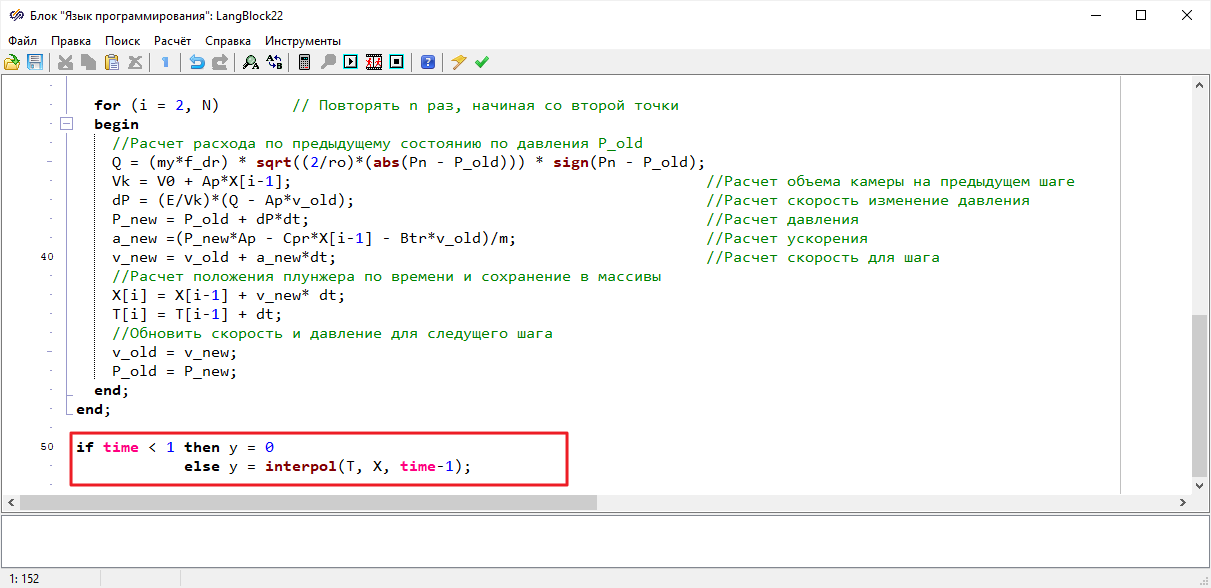
Рисунок 64. Окно скрипта блока «Язык программирования» с отредактированным расчетом свойств
Если теперь запустить проект на моделирование, то получится почти полное
совпадение с моделью, разработанной вручную.
Рисунок 65. Сравнения моделей после редактирование блока «ГПС - Гидравлическая
полость переменного объема»
Промежуточное резюме: Библиотека гидро- пневмосистем в SimInTech значительно
ускоряет работу и обеспечивает большую наглядность модели. В отличие от других
программ САЕ, SimInTech не скрывает от пользователя внутреннее содержание
модели. Она не является "черным ящиком", а скорее практически открытым исходным
кодом для математического моделирования гидравлики. Можно выбирать пакет и
средство моделирования, а затем пытаться реализовать задачу с использованием
специализированных инструментов. Или же можно использовать SimInTech и иметь
возможность решать задачи любым удобным способом. SimInTech не ограничивает
творческую свободу.