АНАЛИЗ УСТОЙЧИВОСТИ НЕЛИНЕЙНЫХ САР С ИСПОЛЬЗОВАНИЕМ МЕТОДА ФАЗОВЫХ ТРАЕКТОРИЙ
Исходные уравнения, особые точки, анализ устойчивости при малом начальном отклонении
В качестве объекта исследования необходимо рассмотреть некоторую абстрактную САР, математическая модель динамики которой описывается следующей системой нелинейных дифференциальных уравнений в форме Коши:
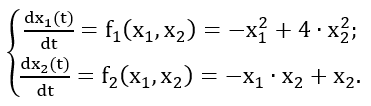
Особые точки находятся из системы при равных нулю левых частях уравнений динамики (условия стационара). Данная динамическая система имеет три особых точки:
1-я точка → (0, 0) → тривиальное решение;
2-я точка → (1, 0.5);
1-я точка → (1, – 0.5).
Для анализа типа особых точек (устойчивое или неустойчивое равновесие) обычно используют линеаризацию уравнений динамики в особой точке и рассматривают поведение линеаризованной системы в малой окрестности особой точки:
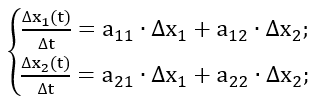
где Δx1=[x1(t)-x01]; Δx2=[x2(t)-x02] – малые отклонения от особой точки;
x01 и x02 – координаты особой точки, а коэффициенты aij вычисляются по соотношениям
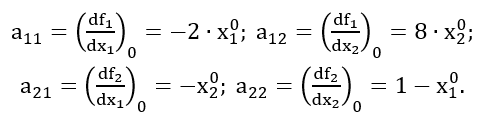
Оценку типа особых точек выполним на основании корней характеристического уравнения, которое для системы записывается в матричном виде:
det(A – λ·E) = 0, где
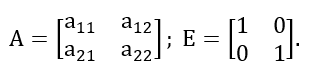
Преобразуя определитель, получаем характеристическое уравнение в виде:
λ2-(a11+a22)⋅λ+(a11⋅a22-a12⋅a21)=0.
Необходимо вычислить корни уравнения для каждой особой точки.
Для первой особой точки коэффициенты равны: а11 = 0; а12 = 0; а21 = 0; а22 = 1. Тогда характеристическое уравнение принимает вид λ2 – λ = 0. По структуре это уравнение соответствует неустойчивому инерционно-интегрирующему звену. Корни уравнения равны «0» и «1» (первый корень – в начале координат; второй корень – в правой полуплоскости).
Положительный корень указывает, что первая точка может быть неустойчивой особой точкой при малом начальном отклонении. Данное утверждение необходимо проверить на этапе анализа результатов прямого расчёта фазовых траекторий.
Для второй особой точки коэффициенты равны: а11 = -2; а12 = 4; а21 = -0.5; а22 = 0. Характеристическое уравнения принимает вид λ2 +2 · λ +2 = 0. Корни этого уравнения равны (-1 ± i), т.е. корни комплексно-сопряженные и лежат в левой полуплоскости.
Резюме: вторая точка является устойчивой при малом начальном отклонении (устойчивый фокус).
Для третьей особой точки коэффициенты равны: а11 = -2; а12 = -4; а21 = 0.5; а22 = 0. Характеристическое уравнения принимает такой же вид, что и для второй точки (λ2 +2 · λ +2 = 0), поэтому корни уравнения равны (-1 ± i). Третья точка является устойчивой при малом начальном отклонении (устойчивый фокус).
Анализ движения автономной системы на фазовой плоскости
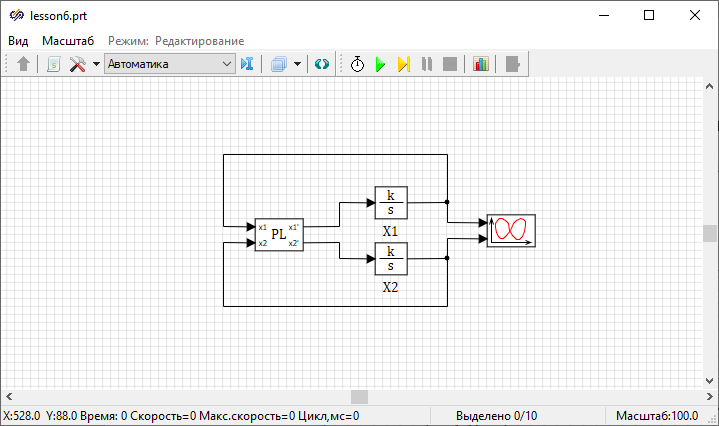
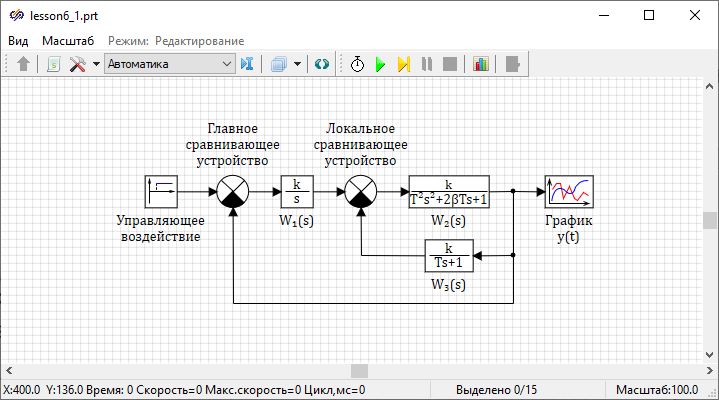
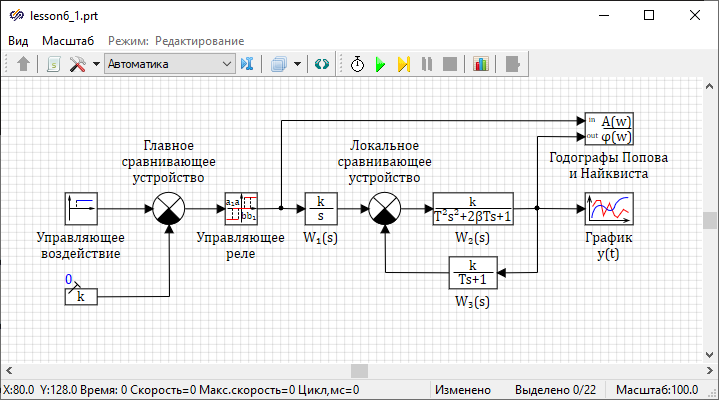
Рисунок 1. Структурная схема САР.
Используя освоенные в предыдущей лабораторной работе методы структурного моделирования для решения обыкновенных дифференциальных уравнений, выполнить в SimInTech решение системы уравнений.
Необходимо сформировать структурную схему для решения системы уравнений согласно рисунку (Рисунок 1).
Для построения фазовых портретов стоит воспользоваться блоком «Язык программирования», который позволяет реализовать численное решение системы дифференциальных уравнений динамики САР, записанной в форме Коши.
Открыть редактор блока «Язык программирования» и заполнить его согласно рисунку (Рисунок 2).
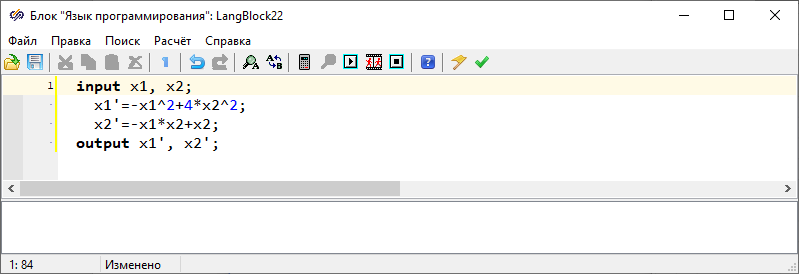
Рисунок 2. Окно редактора блока «Язык программирования».
В свойствах блока с подписью «X1» задать свойство «Начальные условия» равным «-1», а в свойствах блока с подписью «X2» задать свойство «Начальные условия» равным «1». Таким образом была установлена начальная точка на фазовой плоскости с координатами (-1, 1) в начальный момент времени.
В параметрах расчёта проекта установить параметр «Конечное время расчёта» равным «10».
Запустить проект на расчёт и задать вид графиков согласно рисунку (Рисунок 3). Фазовая траектория асимптотически огибает вторую особую точку с координатами (1, 0.5), которая является устойчивым фокусом.
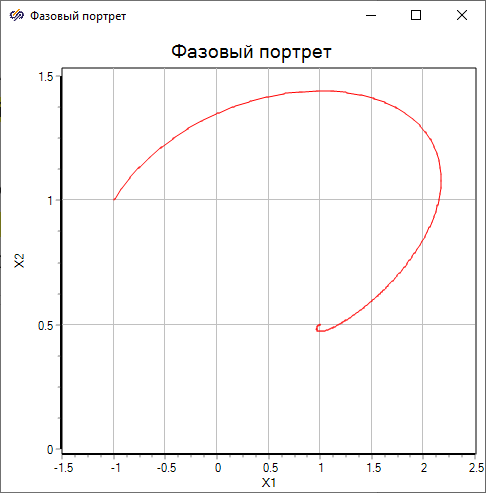
Рисунок 3. Фазовый портрет со стартовой точкой (-1, 1).
В свойствах блока с подписью «X2» задать свойство «Начальные условия» равным «1». Таким образом была установлена начальная точка на фазовой плоскости с координатами (-1, -1) в начальный момент времени.
Запустить проект на расчёт и задать вид графиков согласно рисунку (Рисунок 4). Фазовая траектория асимптотически огибает третью особую точку с координатами (1, -0.5), которая является устойчивым фокусом.
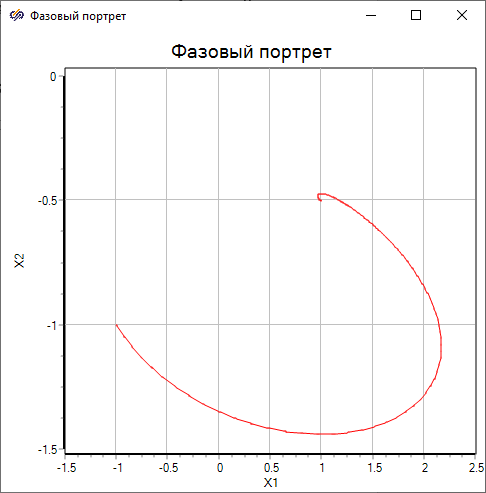
Рисунок 4. Фазовый портрет со стартовой точкой (-1, -1).
Варьируя начальные условия, можно построить и другие фазовые траектории. Однако при необходимости построения большего числа фазовых траекторий для разных начальных условий, процесс варьирования может значительно затянуться, а кроме того, поместить все траектории на один график будет затруднительно. Для реализации таких процессов необходимо выполнить расчет фазовых траекторий в векторизованном варианте, скорректировав собранную схему.
Для одновременного построения большого числа фазовых траекторий необходимо выбрать рассматриваемую часть фазовой плоскости. Пусть x1 ⊂ [-2,4], x2 ⊂ [-3,3].
В рассматриваемой области заданы двадцать начальных точек, координаты которых приведены в таблице (Таблица 1).
| № | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| x1 | -1 | 0 | 1 | 2 | -1 | 0 | 1 | 2 | -1 | 0 | 1 | 2 | -1 | 0 | 1 | 2 | -1 | 0 | 1 | 2 |
| x2 | 2 | 2 | 2 | 2 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | -1 | -1 | -1 | -1 | -2 | -2 | -2 | -2 |
Заполнить редактор блока «Язык программирования» согласно рисунку (Рисунок 5). Такая запись означает, что на вход блока будет подан вектор из двадцати составляющих, сигнал на выходе также будет векторизованным, с той же размерностью.
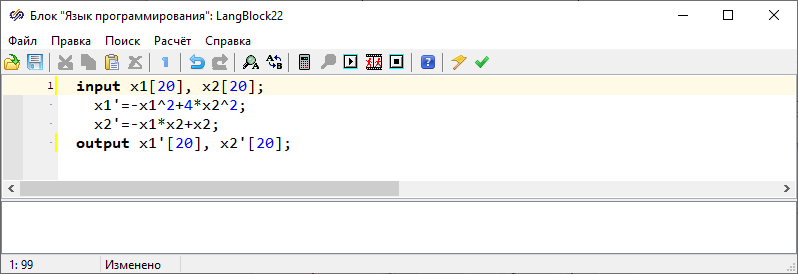
Рисунок 5. Окно редактора блока «Язык программирования».
Открыть окно «Скрипт страницы» и заполнить его согласно рисунку (Рисунок 6), сформировав вектор «х1» и «х2».
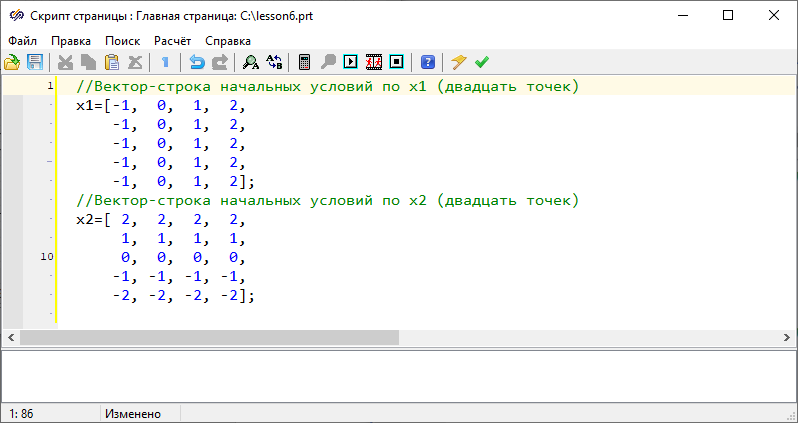
Рисунок 6. Скрипт окна проекта.
В блоке с подписью «Х1» задать свойства «Коэффициент усиления» равным «20#1», свойство «Начальные условия» равным «x1». В блоке с подписью «Х2» задать свойства «Коэффициент усиления» равным «20#1», свойство «Начальные условия» равным «x2».
Запустить проект на расчёт. Группа фазовых траекторий образовало фазовый портрет, вид которого должен быть близким к рисунку (Рисунок 7) и свидетельствовать, что фазовые траектории, начинающиеся строго в верхней полуплоскости стремятся ко второй особой точке с координатами (1, 0.5), а начинающиеся строго из нижней полуплоскости стремятся к третьей особой точке с координатами (1, – 0.5).
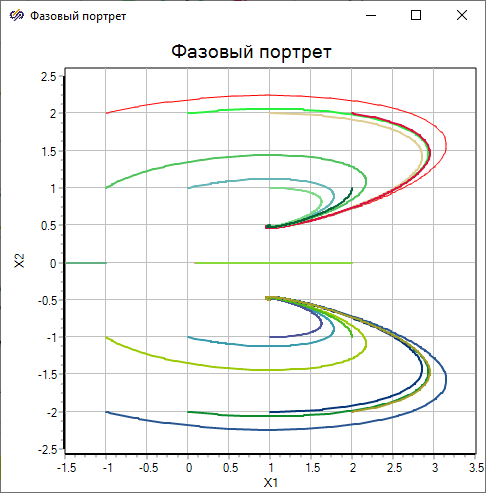
Рисунок 7. Фазовый портрет траекторий.
Фазовые траектории, начинающиеся в точках (1, 0) и (2, 0) с нарастающим замедлением стремятся к первой особой точке (0, 0), а фазовая траектория, начинающаяся из точки (-1, 0) сначала почти неподвижна, а в конце моделирования с нарастающим ускорением устремляется в минус бесконечность.
Для наблюдения за процессом построения фазового портрета необходимо в параметрах расчёта проекта на вкладке «Синхронизация» включить указатель «Синхронизация с реальным временем».
Необходимо увеличить рассматриваемую область фазовой плоскости. Для этого необходимо увеличить каждый элемент массивов «x1» и «x2» в десять раз. Запустить проект на расчёт и задать вид графиков согласно рисунку (Рисунок 8).
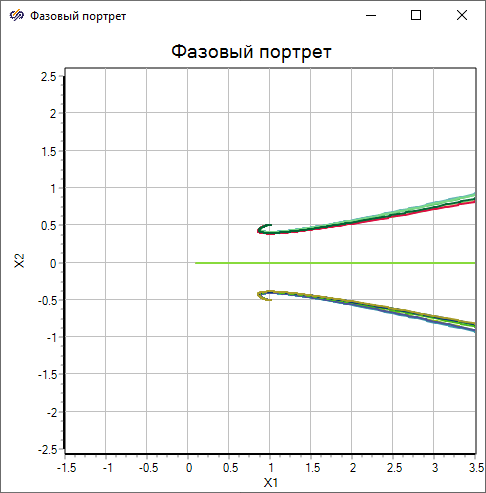
Рисунок 8. Фазовый портрет траекторий.
Практически вся фазовая плоскость (кроме отрицательной оси абсцисс) является областью устойчивых фазовых траекторий. Траектории стремятся обогнуть вторую или третью особые точки.
Резюме: только при отклонении системы в первой особой строго в отрицательную сторону по оси абсцисс нелинейная САР никогда не вернется в какое-то равновесное состояние.