Нечеткая кластеризация


`в палитре`	`на схеме`

Блок реализует процедуру нечеткой кластеризации по одному из алгоритмов, в зависимости от выбранных свойств.

Блок предназначен для поиска центров кластеров – групп из объектов множества входных значений. Входные значения задаются одним из способов, в зависимости от выбранных свойств:

задаются массивы координат входных данных по оси абсцисс и по оси ординат,
задается матрица в текстовом файле: первый столбец матрицы должен соответствовать координатам входных данных по оси абсцисс, второй столбец – координатам входных данных по оси ординат.

Прим.: в файле знаком отделения дробной части должна быть точка, в качестве разделителей между значениями в строке могут использоваться символы «пробел», «табуляция», «;».

Входные значения и найденные центры кластеров отображаются на диаграмме рассеяния, основанной на стандартном блоке вывода графической зависимости Y от X. Для открытия диаграммы рассеяния требуется совершить двойное нажатие левой кнопкой мыши по блоку на схеме.

Поиск центров кластеров происходит по одному из следующих алгоритмов:

Алгоритм нечетких C-средних (Fuzzy C-Means, FCM)
Алгоритм нечетких C-средних — это метод кластеризации данных, который позволяет каждой точке множества принадлежать нескольким кластерам с разной степенью принадлежности.

Метод основан на минимизации целевой функции:
где: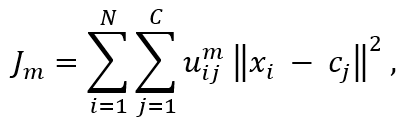

N – количество точек множества входных значений;

C – заданное количество кластеров, на которые необходимо разбить множество;

x_i - i-ая точка множества;

с_j - центр j-го кластера;
u_ij - степень принадлежность x_i к кластеру j;
m - экспоненциальный вес, определяющий нечеткость, размытость кластеров; m > 1, при m → 1, степени принадлежности u_ij стремятся к 0 или 1, что соответствует четкому разбиению на кластеры, обычно принимают m = 2.

Нечеткое разбиение выполняется путем итеративной оптимизации целевой функции с обновлением u_ij и центров кластеров с_j. Алгоритм состоит из следующих шагов:

1. Инициализация степеней принадлежности u_ij случайными значениями.

2. Расчет центров кластеров по формуле:

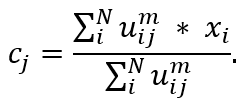
3. Обновление значений степеней принадлежности, согласно формуле:

если ∥x_i - c_i∥ > 0, то

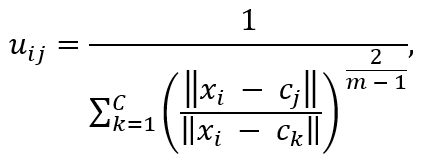
если ∥x_i - c_i∥ = 0, то

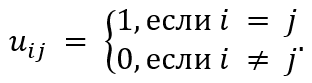
4.Расчет целевой функции J_m

Итерационный процесс не останавливается пока не выполнится условие |J_m+1 - J_m| < ε, где ε - заданный параметр останова алгоритма, либо, пока не будет выполнено указанное максимальное количество итераций.
Субтрактивная кластеризация (Subtractive clustering)
Метод субтрактивной кластеризации основан на поиске «вершин» – точек с максимальными потенциалами, то есть таких, рядом с которыми большое количество других точек множества. Данный алгоритм менее точен, чем алгоритм нечетких С-средних, но и менее требователен к априорной информации: при его использовании не требуется задавать количество кластеров. Алгоритм состоит из следующих шагов:

1. Первоначальное определение потенциалов центров кластеров. За центры кластеров принимаются сами точки и находится потенциал каждой из точек.
где: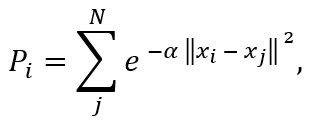

N – количество точек множества входных значений;

x_i, x_j - i-ая и j-ая точки множества соответственно;

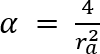, r_a - диапазон влияния, положительная константа, радиус определения соседних точек, точки вне этого радиуса оказывают малое влияние на потенциал данной точки.

Потенциал каждой точки — это функция расстояния до всех других точек. Точка с большим количеством «соседей» будет иметь больший потенциал.

2. Нахождение максимального потенциала P^*₁. Точка с максимальным потенциалом обозначается как первый центр кластеризации -x^*₁.

3. Перерасчет центров кластеров согласно формуле:
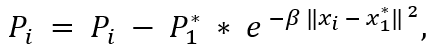где r_b - положительная константа, задающая радиус одного кластера.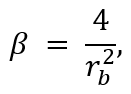

Эта процедура необходима, чтобы исключить влияние на выбор следующего центра кластера от только что найденного кластера. Чтобы избежать получения близко расположенных центров кластеров, значение r_b устанавливают больше, чем r_a:
где η - коэффициент подавления, обычно η = 1.25 или η = 1.5. Меньший коэффициент подавления снижает вероятность того, что точки будут рассматриваться как часть кластера, что приводит к увеличению количества кластеров, и, как следствие, кластерных центров.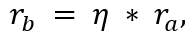

4. Выбор следующего центра кластера как точки, имеющей наибольший потенциал и перерасчет потенциалов точек в соответствии с формулой:
где x^*_k - координата k-го центра кластера, P^*_k - потенциал k-го центра кластера.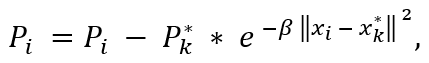
5. Процедура продолжается в соответствии со следующими условиями:
- если
  
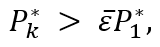
  где ε̅ - коэффициент принятия центра кластера,
  
  то x^*_k принимается как кластерный центр и алгоритм продолжает работу;
- иначе, если
  
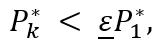
  где ͟ε̲ - коэффициент отклонения центра кластера,
  
  то x^*_k не принимается как кластерный центр и алгоритм прекращает работу;
- иначе, если потенциал попадает в область [ ͟ε̲ * P^*₁, ε̅ * P^*₁], то проверяется, выполняется ли компромисс между достаточным значением потенциала и достаточной удаленностью от существующих центров кластеров, для этого вычисляется кратчайшее расстояние d_min между x^*_k и всеми найденными кластерными центрами и если
  то x^*_k принимается как кластерный центр и алгоритм продолжает работу, иначе x^*_k не принимается как кластерных центр и выбирается следующая точка с наибольшим потенциалом.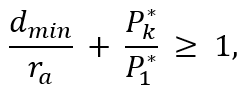

Входные порты

Блок не имеет входов.

Выходные порты

x – векторзначений координат центров кластеров по оси абсцисс;
y – вектор значений координат центров кластеров точек по оси ординат.

Свойства

Способ задания входных данных – выбор способа задания входных данных: «Задать массивы координат», «Считать из текстового файла»;
Массив абсцисс входных данных – массив координат входных данных по оси абсцисс, появляется при выборе способа «Задать массивы координат»;
Массив ординат входных данных – массив координат входных данных по оси ординат, появляется при выборе способа задания «Задать массивы координат»;
Имя файла с матрицей входных данных – строка, содержащая имя файла, в котором содержится матрица входных данных, появляется при выборе способа задания «Считать из текстового файла»;
Алгоритм кластеризации – выбор алгоритма кластеризации: «Алгоритм нечетких С-средних», «Субтрактивная кластеризация»;
Количество кластеров – количество кластеров, центры которых необходимо найти, появляется при выборе алгоритма «Алгоритм нечетких С-средних»;
Параметр остановки итерационного процесса – параметр, определяющий необходимую точность, при достижении которой алгоритм прекратит работу, появляется при выборе алгоритма «Алгоритм нечетких С-средних»;
Максимальное число итераций – параметр, определяющий максимальное число итераций, которое может быть выполнено при невыполнении условия достижения заданной точности, появляется при выборе алгоритма «Алгоритм нечетких С-средних»;
Экспоненциальный вес – экспоненциальный коэффициент нечеткости, определяющий степень размытия границ, появляется при выборе алгоритма «Алгоритм нечетких С-средних»;
Диапазон влияния – положительная константа, задающая радиус определения соседних точек, точки вне этого радиуса оказывают малое влияние на потенциал данной точки, появляется при выборе алгоритма «Субтрактивная кластеризация»;
Коэффициент подавления – скалярная величина, задающая коэффициент масштабирования диапазона влияния, влияющий на значение радиуса кластера, появляется при выборе алгоритма «Субтрактивная кластеризация»;
Коэффициент принятия центра кластера – коэффициент, задающий верхнее пороговое значение, устанавливающее, во сколько раз потенциал данной точки должен быть выше потенциала центра первого кластера, чтобы точка принималась как центр нового кластера, появляется при выборе алгоритма «Субтрактивная кластеризация»;
Коэффициент отклонения центра кластера – коэффициент, задающий нижнее пороговое значение, устанавливающее, во сколько раз потенциал данной точки должен быть ниже потенциала центра первого кластера, чтобы данная точка была отклонена из возможных центров кластеров, должен быть меньше коэффициента принятия, появляется при выборе алгоритма «Субтрактивная кластеризация»;

Параметры

Матрица степеней принадлежности – матрица, содержащая значения степеней принадлежности каждой точки входных данных к каждому из кластеров, имеет размерность (количество точек * количество кластеров), появляется при выборе алгоритма «Алгоритм нечетких С-средних»;
Целевая функция – значение целевой функции, появляется при выборе алгоритма «Алгоритм нечетких С-средних».