Точечная кинетика (модель мгновенного скачка)

Описание

Блок реализует упрощенную модель кинетики нейтронов, а именно: модель мгновенного скачка, дифференциальные уравнения которой получены на основании известных уравнений кинетики "точечного" ядерного реактора в односкоростном приближении.

Блок имеет один входной и один выходной сигнал.

Данный типовой блок соответствует постоянному (во времени) интенсивности внешнего источника нейтронов.

Входные порты

Входным сигналом в блок является абсолютное изменение реактивности ρ(t) - ρ(0).

Выходные порты

Выходным сигналом из блока являются либо безразмерное отклонение нейтронной мощности, либо безразмерная нейтронная мощность.

Свойства

• Эффективная доля запаздывающих нейтронов.
• Начальная подкритичность (в долях β_eff).
• Относительные доли групп запаздывающих нейтронов.
• Постоянные распада групп запаздывающих нейтронов.
• Нормировка (1 – если выход блока нормированная мощность; 0 – если выход блока нормированные отклонения мощности).

Математическая модель

Математическая модель данного блока получена на основании известных уравнений кинетики "точечного" ядерного реактора в односкоростном приближении (т.е. процесс деления ядер осуществляется нейтронами одной энергетической группы – либо только тепловыми, либо только быстрыми):

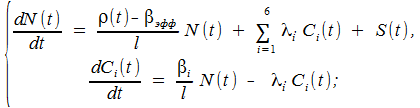
где N(t) – мощность реактора;

ρ(t) – реактивность;

β_eff – эффективная доля запаздывающих нейтронов;

l – время жизни мгновенных нейтронов;

C_i(t) – концентрация ядер-предшественников запаздывающих нейтронов i-й группы;

λ_i – постоянная распада ядер-предшественников i-й группы;

β_i – доля запаздывающих нейтронов i-й группы;

S(t) – интенсивность внешнего источника нейтронов.

Уравнения кинетики нейтронов после преобразований исходной системы уравнений принимают вид:

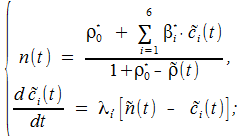
где č_i(t) – нормированное отклонение концентрации ядер-предшественников запаздывающих нейтронов i-й группы;

ρ^*₀ – абсолютная (по модулю) подкритичность ядерного реактора в долях β_eff;

ρ(t) – относительное изменение реактивности в долях β_eff;

β^*_i – относительная доля запаздывающих нейтронов i-й группы.

При t = 0 реактор находится в стационаре, поэтому

Очевидно, что если при t ≤ 0 нейтронная мощность постоянна, то начальные условия для нормированных концентраций ядер-предшественников запаздывающих нейтронов равны 1.0.

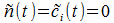
Примечания

1. По умолчанию в первых строках введены параметры, приблизительно соответствующие данным для реактора РБМК-1000.
2. По умолчанию β_i и λ_i соответствуют данным для "чистого" топлива U-235, хотя Пользователь может их скорректировать, например, если в процессе работы реактора нуклидный состав топлива изменился.
3. Структура диалогового окна этого блока позволяет задать и другое число групп ядер-предшественников запаздывающих нейтронов и, соответственно, β_i и λ_i. Например, если необходимо учесть вклад фотонейтронов, то число групп может быть увеличено, например, до 8, и наоборот, можно ввести одногрупповую модель кинетики запаздывающих нейтронов.
4. Если реактор подкритичен, то считается, что его стационарное состояние при t ≤ 0 поддерживалось внешним источником нейтронов.