Рассмотрим алгоритм, представляющий собой комбинацию алгоритмов ЛАРД и АМС – аппроксимированный алгоритм «минимум–сумма» (А–АМС, англ. approximate min–sum, A–Min), отличающийся от ЛАРД меньшим числом операций, выполняемых при расчете сообщений от проверочных узлов [16, 17]. В общем виде для ЛАРД эта операция имеет вид:
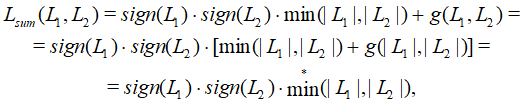
где – функция поиска минимального значения. Таким образом, на шаге об-новления сообщений из проверочного узла требуется найти всего два сообщения – первое для узла, сообщение от которого было минимальным, а второе – для всех остальных узлов.
Алгоритм АМС* использует ту же идеологию – в каждом проверочном узле рассчитывается всего два сообщения – одно для информационного узла, приславшего сообщение с минимальным весом, второе для всех остальных информационных узлов. Отличие заключается лишь в том, что вместо обычного минимума из двух аргументов используется оператор ![]() , в котором помимо операции поиска минимума используется еще и функция корректировки g(L1, L2)
, в котором помимо операции поиска минимума используется еще и функция корректировки g(L1, L2)
В обобщенном виде этот алгоритм выглядит следующим образом.
1 шаг. Инициализация декодера. Для всех узлов i инициализируются значения Li в зависимости от используемой модели канала связи:
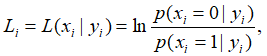
2 шаг.Обновление проверочных узлов. Для всех проверочных узлов CN вычислить исходящие сообщения Lj→i для узла с минимальной достоверностью:
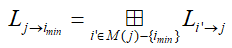
для всех остальных:
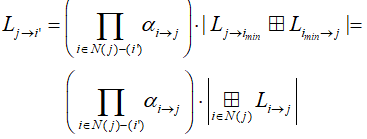
и передать их соответствующим информационным узлам VN.
3 шаг.Обновление битовых узлов. Вычислить сообщения Li→j , исходящие от информационных узлов VN:
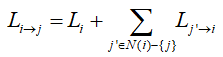
и передать их соответствующим проверочным узлам.
4 шаг. Вычисление апостериорных ЛОП. Для всех j=0,1...,N-1 вычислить:
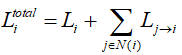
5 шаг. Получение жестких решений. Для всех i=0,1...,N-1 найти жесткие решения:
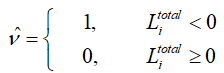
6 шаг.Проверка правильности декодирования. Вычислить синдром:
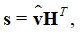
Подобная модификация позволяет снизить вычислительные затраты на вычисление сообщений из проверочного узла для АРД-подобных алгоритмов с 3(dc-1) до (dc-1) операции ⊞. По эффективности этот алгоритм занимает промежуточное место между АРД-подобными алгоритмами и алгоритмом АМС.
В алгоритме используется оператор ⊞, а значит, при реализации может быть использована любая его интерпретация. Видно, что алгоритм сводится к поиску всего двух отсылаемых сообщений вместо dc. Вычисление этих двух сообщений займет dc-1 арифметических операций. Правомерность применения такого упрощения можно пояснить, рассмотрев работу алгоритмов АРД и АМС. Если при декодировании проверочного узла два или более входящих в проверочный узел сообщений недостоверны, то недостоверными будут все сообщения, исходящие из этого узла. Это свойство сохраняется и при введении рассматриваемой модификации. Если всего одно входящее в проверочный узел сообщение не верно, то исходящее сообщение для недостоверного информационного узла будет достоверным для всех трех декодеров. Как видно из описания рассматриваемого упрощения, в обоих рассмотренных случаях сообщение, отправляемое к самому ненадежному информационному узлу, всегда будет в точности таким же, как и для алгоритма АРД.
Обобщенный алгоритм МС*
В общем виде выражение для обновления проверочных узлов, для обобщенного алгоритма ОАМС*, примет вид:
Для узла с минимальной достоверностью:
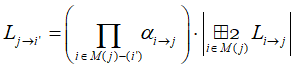
для всех остальных:
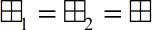
Видно, что частный случай АМС*, при ⊞1 требует меньших затрат на реализацию чем ОАМС*, поскольку вторая сумма, для оставшихся узлов, может быть найдена из первой, как это сделано выше. Что позволяет выполнить обновление проверочных узлов за (dr-1) операции ⊞. В обобщенном алгоритме на это требуется (dr-2) операции
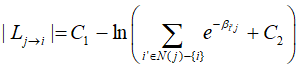
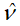 , что больше чем
для АМС*, но меньше, чем для классической схемы реализации АРД-подобных алгоритмов
декодирования, а следовательно подобная реализация имеет право на жизнь и требует
дополнительного исследования. Обобщенное представление алгоритма АМС* позволяет получить еще
одну модификацию, не очевидную при анализе частного случая АМС*.
, что больше чем
для АМС*, но меньше, чем для классической схемы реализации АРД-подобных алгоритмов
декодирования, а следовательно подобная реализация имеет право на жизнь и требует
дополнительного исследования. Обобщенное представление алгоритма АМС* позволяет получить еще
одну модификацию, не очевидную при анализе частного случая АМС*.
Модификация МОАМС (ma-min)
Основой алгоритма является тот факт, что необходимым условием для вычисления
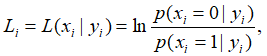
является нахождение индекса проверки с минимальным весом imin, а следовательно
можно найти вес минимальной проверки всего за одно обращение к памяти. То есть в данном случае
в качестве ![]() используется реализация ⊞2, поскольку в этом случае
используется реализация ⊞2, поскольку в этом случае ![]() есть
ни что иное как оператор поиска минимального значения среди весов проверок.
есть
ни что иное как оператор поиска минимального значения среди весов проверок.
Таким образом, получаем модификацию ОАМС* алгоритма, требующего (dr-2) операции 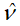 и 1 операцию обращения к памяти, что меньше чем для алгоритма АМС*. Обозначим его как МОАМС* - минимальный ОАМС*.
и 1 операцию обращения к памяти, что меньше чем для алгоритма АМС*. Обозначим его как МОАМС* - минимальный ОАМС*.
Сопутствующие материалы:
- Витязев В.В., Лихобабин Е.А. Алгоритмы декодирования кодов с низкой плотностью проверок на четность, основанные на структуре алгоритма «минимум-сумма» // Успехи современной радиоэлектроники. – 2014. – №6. – С. 26-35.
- Vityazev V., Likhobabin E., Ustinova E., “Min-Sum Algorithm-Structure Based Decoding Algorithms for LDPC Codes”, 3rd Mediterrian Conference on Embedded Computing, Budva, Montenegro. –2014, June. – pp. 256-259.
- Jones C., Valles E., Smith M., Villasenor J. Approximate-min* constraint node updating for LDPC code decoding // IEEE Military Communication Conference. – 2003, October. – pp. 157-162.
- Витязев В.В., Лихобабин Е.А. Алгоритмы декодирования кодов с низкой плотностью проверок на четность, основанные на алгоритме «минимум-сумма» // Труды РНТОРЕС имени А.С.Попова. Серия: Цифровая обработка сигналов и ее применение – М.Выпуск XVI-1. – 2014. – С.117-121.
