Алгоритм декодирования LDPC MSA (АМС)

Алгоритм минимальной суммы (АМС, Min-Sum Algorithm) является дальнейшим упрощением алгоритма Алгоритм декодирования LDPC LLR BP (ЛАРД). Математически АМС можно рассматривать как упрощение аппроксимаций выражения сложения двух ЛОП в декодере проверочных узлов:



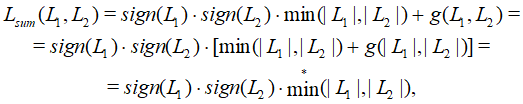
Алгоритм ограничивается вычислением только первого слагаемого этого выражения:



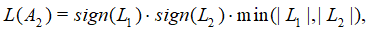
что может быть оправданным, поскольку |g(L1,L2)| ≤ 0,693.

Максимальная погрешность при переходе к упрощенной реализации максимальна для близких по значению аргументов. Для больших входных значений, то есть больших ЛОП, что соответствует каналу с малым уровнем шума, разница между упрощенной и не упрощенной реализациями мала.

Дополнительным достоинством такого упрощения является тот факт, что значение исходящего сообщения для каждого информационного узла может быть вычислено нахождением всего двух минимальных значений достоверностей, входящих в проверку, плюс вычисление его знака:



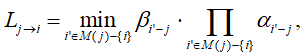
где α - знак, β – модуль сообщения от i-го информационного узла к j-му проверочному узлу.

Второе достоинство заключается в том, что при использовании модели канала с АБГШ инициализация может осуществляться не канальными ЛОП, а принятыми из канала амплитудами соответствующих бит. Это обусловлено выражением вычисления значений ЛОП для АБГШ L = 4yn/σ2, yn - принятый зашумленный сигнал, σ2 – дисперсия шума. Поскольку из вычислений удалена нелинейная функция g(L1, L2), то результаты вычислений для L и yn будут совпадать с точностью до множителя L=4/σ2 . Таким образом, для алгоритма АМС отпадает необходимость в получении оценки отношения сигнал/шум на входе.

В силу этой особенности алгоритм также известен [2] как алгоритм распространения доверия по равномерно наиболее мощному критерию (uniformly most powerful belief propagation, UMP-BP).

В обобщенном виде алгоритм АМС можно представить в виде шести шагов.

Шаг 1. Инициализация. Для всех узлов i инициализировать значения Li по формуле:



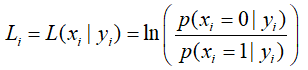
в зависимости от используемой модели канала связи. Затем для всех сообщений, исходящих из информационного узла i к узлам j, устанавливается Li→j = Li.

Шаг 2. Обновление проверочных узлов. Для всех проверочных узлов CN вычислить исходящие сообщения Lj→i по формуле:



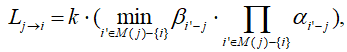
где k - коэффициент для аттенюации сообщений от проверок к битам, и передать их соответствующим информационным узлам VN.

Шаг 3. Обновление информационных узлов. Вычислить сообщения Li→j, исходящие от информационных узлов VN:



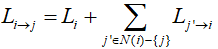
и передать их соответствующим проверочным узлам.

Шаг 4. Вычисление апостериорных ЛОП. Для всех j = 0, 1, …, N-1 вычислить:



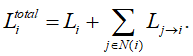
Шаг 5. Получение жестких решений. Для всех j = 0, 1, …, N-1 найти жесткие решения:



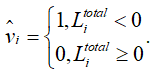
Шаг 6. Проверка условия остановки. Вычислить синдром:



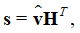
где H - проверочная матрица LDPC кода. Если s = 0 или число итераций достигло максимума – вычисления прекращаются, а полученное жесткое решение считается результатом декодирования, в противном случае вычисления продолжаются с шага 2.

Отличие алгоритма MSA от MSA+Self-Correction заключается в шаге 3 – обновлении информационных узлов. Для MSA+Self-Correction 3 шаг имеет вид:

Для всех информационных узлов VN вычисляются исходящие сообщения Li→j, а затем передаются соответствующим проверочным узлам CN:



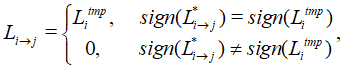
где L*i→j - сообщение Li→j с предыдущей итерации декодирования, а Ltmpi вычисляется по формуле:



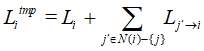
Кроме модификации Self-Correction для алгоритма MSA можно использовать аттенюацию передаваемых сообщений между узлами с помощью коэффициента аттенюации k на шаге 2. Введение данного коэффициента позволяет увеличить эффективность декодирования для некоторых LDPC кодов. Значение коэффициента подбирается аналитически.

Сопутствующие материалы

  1. Chen J., Dholakia A., Eleftheriou E., Fossorier M., Hu X.Y. Near optimal reduced-complexity decoding algorithms for LDPC codes // Proceedings IEEE International Symposium on Information Theory, Lausanne, Switzerland. – 2002, July.
  2. Fossorier M., Mihaljevich M., Imai H. Reduced complexity iterative decoding of low-density parity check codes based on belief propagation, IEEE Transactions on Communications. – 1999, May. – Vol. 47. – № 5. – pp. 673-680.
  3. Лихобабин Е.А. Упрощенные алгоритмы декодирования кодов с низкой плотностью проверок на четность, основанные на алгоритме распространения доверия // Цифровая обработка сигналов, № 3, 2013. С. 74-81.